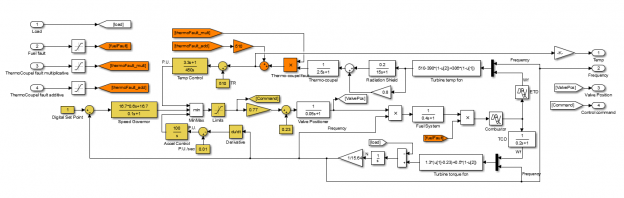
В статье предложена иерархическая модель процесса нейросетевого диагностирования систем управления турбоагрегатами. Выделены два уровня обработки данных, которые последовательно оценивают степени принадлежности симптомов к каждой из потенциальных неисправностей и ставят диагноз техническому состоянию. Для ускорения обучения нейронной сети предложен метод многоэтапного тренинга. На примере системы управления газовой турбиной анализируется эффективность предложенной архитектуры интеллектуального диагностического аппарата с сетью прямого распространения и LSTM-сетью.
Доклад представлен на международной научной конференции «IEEE Northwest Russia Conference On Mathematical Methods In Engineering And Technology: ММEТ NW 2018»