Начинаем серию статей, посвященных автоколебаниям с точки зрения теории управления. Статьи рассчитаны на подготовленного читателя и несут значительную теоретическую нагрузку, хотя и не включают полного аналитического обоснования всех положений.

Автоколебания — это периодические процессы в нелинейных системах, часто встречаются в системах. В практике автоматического управления важен автоколебательный режим систем. В нелинейных системах, в отличии от линеаризованных моделей при потере устойчивости не возникает неограниченного роста значений переменных состояния, а при колебательном характере неустойчивости колебания расходятся до амплитуды, определяемой параметрами системы. Кроме того, автоколебательные режимы часто используются для регулирования различных физических параметров технологических процессов, например температуры. При этом учитываются ограничения на допустимые частоты и амплитуды колебаний.

Определение точной формы и параметров периодических режимов возможно только для некоторых типов систем, например релейных. Наиболее удобным способом исследования предельных циклов в системах второго (и, иногда, третьего) порядков — метод фазовой плоскости. Однако, такой подход практически невозможен для большинства систем, описываемых моделями высоких порядков со сложными нелинейностями.

Один из способов получения информации о существовании и параметрах автоколебательных режимов — метод гармонического баланса.

Метод гармонического баланса

Основные положения

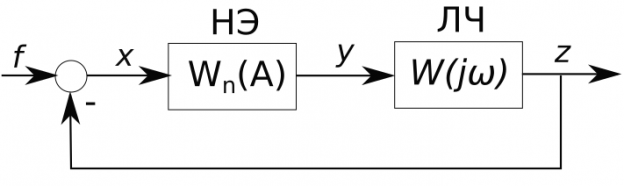
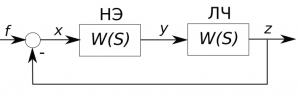
Пусть имеется нелинейная модели автономной системы, представленная структурной схемой расчетного вида и имеется задача исследования собственных периодических колебаний.

Параметризация решения

Для упрощения задачи принимается решение о форме решения, т.е. искомое решение параметризуют.

Предположим, что характер поведения переменной на входе \(x(t)\) нелинейного элемента периодичен, а форма сигнала близка к гармонической:

\[ x(t)= A sin(\omega t) \]

Анализ условия прохождения сигнала

Примем гипотезу фильтра о гармонической форме искомого периодического движения. Предположим, что амплитуды высших гармоник на входе нелинейного элемента и выходе линейной части малы в силу фильтрующих свойств линейной части.

Еще одно необходимое условие метода — малость влияния высших гармоник на условие баланса амплитуд и фаз.

Подход 1. Передаточные функции

Следующим шагом является анализ прохождения гармонического сигнала по контуру, образованному нелинейным элементом, линейной частью и элементом сравнения. Допустим, что периодический сигнал на выходе нелинейного элемента

\[ y(t) = F(x(t))\]

имеет тот же период, однако может содержать высшие гармоники, которые также проходят через линейную часть с передаточной функцией \(W(s)\), которая ослабляет их в большей степени, чем первую гармоническую составляющую, согласно гипотезе фильтра. Исходя из этого в составе переменной \(z(t)\) их доля мала:

\[ z(t) = A_z sin(\omega t + \phi_z)\]

Учитывая отрицательную обратную связь, изменяющей фазу сигнала на \(-\pi\) радиан, условием существования автоколебаний в контуре является баланс амплитуд и фаз:

\[ A_z = A \\
\phi_z = -\pi \]

Тогда комплексный коэффициент передачи линейной части по гармонической составляющей выражается следующим образом:

\[ W(j \omega) = R(\omega) e^{j \phi(\omega)}\]

Аналогично примем, что преобразование гармонического сигнала безынерционным нелинейным элементом описывается комплексным коэффициентом передачи (описывающей функцией):

\[ W_n (A) = R_n (A) e^{j \phi_n(A)}\]

где \(R_n (A)\) — отношение амплитуды первой гармонической составляющей сигнала \(y(t)\) к амплитуде \(A\) входного сигнала; \(\phi_n(A)\) — фазовый сдвиг первой гармоники по отношению к входному сигналу.

Исходя из этого, при прохождении гармонического сигнала через последовательно соединенные нелинейный элемент и линейную часть его амплитуда изменяется в \(R(\omega) R_n(A) \) раз, а сдвиг фаз равен \(\phi (\omega)+\phi(A)\).

В рассматриваемой нелинейной системе возможно существование переодических колебаний, если при прохождении гармонического сигнала по контуру сохраняется значение амплитуды, а фазовый сдвиг с учетом элемента сравнения равен \(— \pi \), т.е. выполняются следующие условия:

\[ R_n(A)R(\omega) = 1\]

\[ phi_n(A) + \phi(\omega) = -\pi\]

Подход 2. Критерий Найквиста

Получить условия возникновения автоколебаний можно иначе.

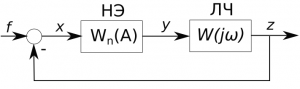
Ниже изображена структурная схема гармонически линеаризованной системы, эквивалентной исходной для множества гармонических сигналов на входе нелинейного элемента и при выполнении гипотезы фильтра.

Особенностью такой модели является неполная определенность ее параметров, зависящих от искомой амплитуды \(A\) и частоты \(\omega \). В исходной системе возможны автоколебания, если в эквивалентной системе устанавливаются гармонические колебания, т.е. параметры линеаризованной системы соответствуют колебательной границе устойчивости. В соответствии с критерием Найквиста условие нахождения значений параметров линеаризованной системы, заданной частотными характеристиками звенев, на границе устойчивости выражается следующим образом:

\[ W_n(A)W(j\omega) = -1\]

из этого выражения с учетом комплексного коэффициента передачи линейной части и преобразования гармонического сигнала нелинейным элементом вытекают эквивалентные условия баланса амплитуд и фаз.

Полученные условия представляют собой систему нелинейных уравнений относительно частоты \(\omega\) и амплитуды \(A\) искомой первой гармоники колебаний переменной \(x(t)\).

В общем случае баланс может устанавливаться с учетом постоянного смешения \(x_0\) гармонического сигнала на входе нелинейного элемента и конечного числа высших гармоник.

Для сложных систем нелинейных уравнений с большим числом переменных, как правило, не существует аналитического решения или оно чрезмерно сложно для ручной обработки и для их решения разумно использовать численные или аналитические методы расчета на ЭВМ.

В случае принятия гипотезы о близости формы искомых колебаний к гармоническим основными этапами метода гармонического баланса являются:

Замена нелинейного элемента эквивалентной характеристикой (гармоническая линеаризация)
Определение параметров колебаний
Анализ чувствительности решения к высшим гармоникам и малым параметрам системы.

Источник

Теория автоматического управления: Учеб. для вузов/С.Е. Душин, Н.С. Зотов, Д.Х. Имаев и др.; Под ред. В.Б. Яковлева. — М.: Высшая школа, 2003. — 567 с.

Digiratory

Лаборатория автоматизации и цифровой обработки сигналов

Автоколебания. Введение