Во второй части рассмотрим гармоническую линеаризацию нелинейного элемента, которая, по сути, является поиском эквивалента нелинейного элемента для некоторого множества гармонических сигналов. В рассмотрении ограничимся симметричными колебаниями.

\[ x(t)= A sin(\omega t) \]

Коэффициенты гармонической линеаризации определяются как отношение первых гармонических составляющих выхода нелинейного элемента к амплитуде входа:

\[ q(A, \omega) = \frac{\alpha}{A} = \frac{1}{TA} \int_0^T F(A sin(\omega t)) sin(\omega t) dt \\
q’(A, \omega) = \frac{\beta}{A} = \frac{1}{TA} \int_0^T F(A sin(\omega t)) cos(\omega t) dt, \]

где \(\alpha \) и \(\beta \) —коэффициенты разложения Фурье по косинусной и синусной составляющим. Из приведённых формул следует, что гармоническая линеаризация дает усредненные за период свойства нелинейного элемента по преобразованию гармонического сигнала.

Опуская вывод, эквивалентная комплексная характеристика записывается следующим образом:

\[ y_1(t) = [q(A)+ \frac{p}{\omega q’(A)}]x(t) \]

Выражение в квадратных скобках является эквивалентным оператором нелинейного элемента. Кроме того, можно записать эквивалентную передаточную функцию:

\[ W_n(A,S) = q(A)+ \frac S \omega q’(A) \]

и эквивалентную частотную характеристику (\(S=j \omega\)):

\[ W_n(A) = q(A) + jq’(A) = R_n(A) exp(j \phi_n(A)) \]

модуль и аргумент которой записываются так:

\[ R_n(A) = sqrt(q^2(A) + [q’(A)]^2)\]

\[ phi_n = arctg(\frac{q’(A)}{q(A)})\]

Способ вычисления коэффициентов линеаризации

Для динамических нелинейных элементов установившийся сигнал при гармоническом входе с конкретными значениями \(A\) и \(\omega\) определяется путем численного решения дифференциальных уравнений, после чего находят значения \(q(A, \omega)\) и \(q’(A, \omega)\). Таблица коэффициентов гармонической линеаризации находится путем многократного повторения операции.

Кроме того, возможно вычисление коэффициентов безынерционных нелинейных элементов усреднением по фазе и множеству значений входа.

Вычисление коэффициентов гармонической линеаризации усреднением по фазе

В частном случае безынерционных нелинейностей коэффициенты гармонической линеаризации не зависят от частоты. Поэтому от усреднения по времени можно перейти к усреднению по фазе:

\[ q(A, \omega) =\frac{\alpha}{\pi A} = \frac 1{TA} \int_0^{2\pi} F(A sin(\psi)) sin(\psi) d\ psi \\
q’(A, \omega) = \frac{\alpha}{\pi A} = \frac 1{TA} \int_0^{2\pi} F(A sin(\psi)) cos(\psi) d\theta \]

Практическое значение сводится к получению периодического сигнала

\[ y(\psi) = F(A sin(\psi))\]

и вычислению интегралов.

Пример расчета

Рассмотрим алгоритм на примере задачи получения коэффициентов гармонической линеаризации идеального релейного элемента. Периодический сигнал \(y(\psi)\) при гармоническом сигнале на входе представляет собой прямоугольные колебания с уровнями \(\pm C\)

\[ y(\psi) = C, 0<= \psi<\pi –C, \pi <= \psi < 2 \pi \]

Подставляя в формулы расчета коэффициентов:

\[ q(A) = \frac{1}{\pi A} (\int_0^{\pi} C sin(\psi) d \psi – \int_{\pi}^{2\pi}C sin(\psi) d \psi) = \frac{C}{\pi A} (-cos(\psi) \bigg |_0^{\pi}) + cos(\psi) \bigg |_{\pi}^{2\pi}) = \frac{4C}{\pi A} \]

\[ q’(A) = \frac{1}{\pi A} (\int_0^\pi C cos(\psi) d \psi – \int_\pi^{2\pi}C cos(\psi) d \psi) = \frac{C}{\pi A} (sin(\psi) \bigg |_0^{\pi}) — sin(\psi) \bigg |_{\pi}^{2\pi}) = 0 \]

Тогда эквивалентная характеристика идеального реле равна \(q(A)\):

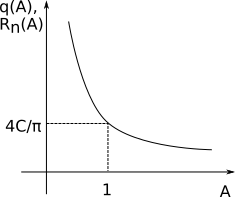
\[ R_n (A) = \frac{4C}{\pi A} \]

а фазовые сдвиги равны нулю, т.е. фаза первой гармонической составляющей выхода совпадает с фазой входа.

Особенность безынерционного нелинейного преобразования такого рода — дискриминация сигналов по уровню. Это хорошо видно, если построить график усиления в зависимости от амплитуды.

Источник

• Теория автоматического управления: Учеб. для вузов/С.Е. Душин, Н.С. Зотов, Д.Х. Имаев и др.; Под ред. В.Б. Яковлева. — М.: Высшая школа, 2003. — 567 с.

Оглавление

1. Автоколебания. Введение
2. Автоколебания. Гармоническая линеаризация
3. Автоколебания. Определение параметров периодических режимов
4. Автоколебания. Устойчивость