В статье предложена иерархическая модель процесса нейросетевого диагностирования систем управления турбоагрегатами. Выделены два уровня обработки данных, которые последовательно оценивают степени принадлежности симптомов к каждой из потенциальных неисправностей и ставят диагноз техническому состоянию. Для ускорения обучения нейронной сети предложен метод многоэтапного тренинга. На примере системы управления газовой турбиной анализируется эффективность предложенной архитектуры интеллектуального диагностического аппарата с сетью прямого распространения и LSTM-сетью.

Доклад представлен на международной научной конференции «IEEE Northwest Russia Conference On Mathematical Methods In Engineering And Technology: ММEТ NW 2018»

I. ВВЕДЕНИЕ

Диагностирование систем управления (СУ) техническими объектами с помощью экспертных моделей, ставящих диагнозы на основе пороговых значений переменных, ограничивает объем информации, используемой для анализа состояния объекта. Использование отрезков временных рядов в качестве диагностических признаков увеличивает объем обрабатываемых данных об анализируемом объекте, однако непосредственный перенос экспертных знаний к выборкам является труднореализуемой задачей. В качестве компромисса предлагается использовать интеллектуальные технологии (методы машинного обучения), в частности, нейросетевые диагностические модели [1]–[3]. Обучаемые искусственные нейронные сети, хорошо зарекомендовавшие себя в задачах бинарной классификации, менее эффективны в задачах диагностирования, как правило, связанного с многоальтернативной классификацией ситуаций.

Предлагается подход к разработке нейросетевых интеллектуальных диагностических систем с бинарными классификаторами на первом уровне и итоговым классификатором — на втором. Анализируется эффективность использования нейронных сетей прямого распространения и рекуррентных сетей типа LSTM [4] в диагностических моделях первого уровня. В качестве примера объекта исследования выбрана одна из первых моделей систем управления турбоагрегатом, разработанная W. Rowen [5] для удовлетворения спроса на точные математические модели газовых турбин большой мощности фирмы General Electric.

II. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СИСТЕМЫ УПРАВЛЕНИЯ

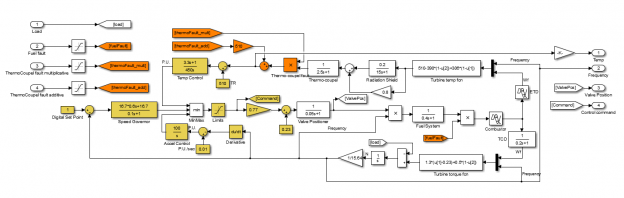
Структурная схема СУ турбоагрегата [5] (рис. 1) несколько упрощена. Значения параметров соответствуют модели газовой турбины типа GE 7001B. Переменные (за исключением температуры) нормированы относительно номинальных значений. Пределы применимости модели ограничиваются диапазоном 95…107 % от номинальной частоты вращения турбины, за пределами которого линейная модель турбины перестает быть адекватной или возможны разрывные управляющие воздействия.

Правая часть структурной схемы (см. рис. 1) представляет модель собственно турбины: наверху — блоки, описывающие изменения температуры выхлопных газов и измерения температуры; по центру схемы — топливная подсистема, включающая в себя топливный клапан, компрессор и камеру сгорания; в нижней части структурной схемы представлены уравнения связи крутящего момента, частоты вращения ротора, момента нагрузки и расхода сжигаемого топлива. Левая часть структурированной модели содержит регулятор, состоящий из трех компонентов: управления частотой вращения, температурой и ускорением. Последние два компонента регулятора выполняют предохранительную функцию – предотвращают перегрев или чрезмерные ускорения турбины. Заметим, хотя модель турбины в работе [5] заявлена как линейная, в ней присутствуют нелинейность типа «минимум» и блок умножения.

Неисправности канала измерения температуры выхлопных газов могут быть как мультипликативными, так и аддитивными. Неисправности канала подачи топлива являются мультипликативными – «жесткими», которые моделируются скачкообразным изменением соответствующих коэффициентов уравнений, или «мягкими», которые сводятся к плавным изменениям параметров. Выделяется 6 классов неисправностей: жесткая и мягкая мультипликативные неисправности топливной системы; жесткая и мягкая мультипликативные неисправности термопары; жесткая и мягкая аддитивные неисправности термопары. Если модель W. Rowen [5] дополнить моделями потенциальных вышеперечисленных неисправностей, а к измеряемым выходам подключить устройства выявления симптомов и постановки диагноза, то получится так называемая диагностическая модель [2] СУ газовой турбиной (см. рис. 1).

III. НЕЙРОСЕТЕВАЯ ДИАГНОСТИЧЕСКАЯ МОДЕЛЬ

Пусть система может иметь N потенциальных неисправностей, т. е. с учетом исправной системы необходимо решить задачу классификации множества состояний на N+1 класс.

Предлагается двухуровневая архитектура нейронной сети. Первый уровень состоит из N обучающихся независимо друг от друга подсетей, которые выявляют степень принадлежности текущего состояния к соответствующей неисправности, т. е. симптомы.

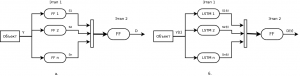
Обученные независимо нейронные сети могут иметь пересечения классов неисправностей, формируя ложноположительную принадлежность к своему классу при данных на входе, соответствующих неизвестному классу состояния объекта. Несмотря на этот недостаток, обучение нейронной сети на двух классах значительно проще, что позволяет использовать относительно небольшие сети прямого распространения (FF- сети). Для компенсации эффекта интерференции классов неисправностей вводится второй уровень нейронной сети, входами которой оказываются выходы 2N подсетей первого уровня. На рис. 2 представлены структуры нейросетевых моделей диагностирования с сетью прямого распространения для выделения симптомов (рис. 2, а) и LSTM-сетью (рис. 2, б). Заметим, что в отличие от сети прямого распространения, где вход – отрезок временной последовательности, у LSTM-сети, являющейся рекуррентной, на входе мгновенные значения наблюдаемых параметров.

Нейросетевая модель диагностирования обучается в несколько этапов: на первом этапе происходит обучение нейронных сетей первого уровня и значения их весов фиксируются; далее обучается полная нейросетевая модель путем подстройки весов сети второго уровня.

A. Подготовка данных для обучения нейронных сетей

Так как цель диагностирования состоит в обнаружении, локализации и идентификации неисправностей, в том числе, мягких – сводящихся к относительно медленным изменениям параметров объекта, – то для постановки диагноза необходимо использовать данные о поведении объекта в виде временных рядов.

Для генерирования обучающих данных используется Simulink-модель СУ турбиной и специально созданные подпрограммы (m-файлы) – для автоматизации подготовки обучающих последовательностей. Процессы создания, обучения и тестирования нейронной сети в Keras и TensorFlow [6] на языке Python автоматизированы и с минимальными изменениями могут использоваться для других целей машинного обучения.

Приняты следующие ограничения на модели неисправностей: интенсивность жестких неисправностей (множитель) принадлежат диапазону [0, 0.1], интенсивность мягких неисправностей – диапазону [0, 0.01]. Таким образом, рассматриваются только те неисправности, которые не приводят к отказам, остановке (аварии) в краткосрочной перспективе и могут достаточно долго оставаться незамеченными. Кроме того, для большего разнообразия данных момент нагрузки турбоагрегата, время наступления неисправности и интенсивность неисправности принимаются случайными величинами, различными для каждой итерации моделирования.

Данные компьютерной имитации разделены на блоки по 100 секунд (100 отсчетов), соответствующие в случае использования сетей прямого распространения группе входов из 100 элементов и 100 тактам работы сети – при использовании рекуррентной нейронной сети, как при ее обучении, так и при тестировании.

B. Обучение нейронной сети

В первую очередь обучаются нейронные сети, предназначенные для выявления принадлежности состояния объекта к одному из классов неисправности. Таким образом, обучение модели производится в N+1 этап, где N — число рассматриваемых неисправностей. Такой подход позволяет добиться большой точности классификации на первом уровне классификатора и почти полностью исключить ложноположительные срабатывания.

IV. РЕЗУЛЬТАТЫ ДИАГНОСТИРОВАНИЯ СУ ТУРБОАГРЕГАТА

Основной задачей исследования стоит проверка эффективности предложенной архитектуры нейросетевой модели и выбор наиболее эффективного типа нейронной сети для первого уровня модели. Исходя из этого, рассмотрим качество диагностирования для двух рассматриваемых архитектур, обучаемых на выборках одинакового размера. Ключевыми критериями качества является точность диагностирования и доля ложноположительных срабатываний.

A. FF-сеть

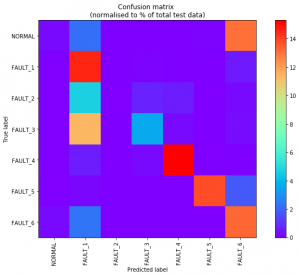
По итогам обучения нейронной сети прямого распространения при распознавании 6 типов неисправностей СУ газовой турбиной получена точность 64%. Кроме того, в валидации получена «Confusion matrix» (рис. 3), строки которой отвечают истинным значениям, а столбцы — выходам сети. Клеткам матрицы отвечает число совпадений. Хорошим результатом валидации является преобладание диагональных элементов. В нашем случае, показывающей объединение классов исправного состояния системы и наличия неисправности 1 – «Жесткая мультипликативная неисправность топливной системы». Наблюдается значительное количество ложноположительных срабатываний с диагнозом 6 – «Мягкая аддитивная неисправность термопары» при исправном СУ, что, вероятно, связано с характером проявления неисправности. Также имеется значительное число ложноотрицательных срабатываний (с учетом объединения исправного состояния и неисправности 1).

Отметим, что при использовании сетей прямого распространения эквивалентного размера для непосредственного диагностирования всех рассматриваемых состояний СУ турбиной достигнута точность менее 17%.

B. LSTM-сеть

При обучении рекуррентной нейронной сети заметны преимущества на первом этапе диагностирования — качество обученной сети менее чувствительно к выбору начальных параметров, а также обеспечивается большая точность постановки диагноза.

Точность многоклассового диагностирования при использовании в качестве бинарного классификатора LSTM-сети составила 67%. При анализе «Confusion matrix» видно, что наблюдается ситуация с объединениями классов эквивалентная FF-сети. Кроме того, при проверке эффективности LSTM-сети при одноуровневой архитектуре нейросетевого аппарата диагностирования получена схожая точность ~ 65%.

V. ЗАКЛЮЧЕНИЕ

Предложенная архитектура диагностирования, использующая многоуровневые моделей с предварительным обучением на подзадачах выявления симптомов, повышает эффективность и сходимость процесса обучения при диагностировании с помощью сетей прямого распространения. Вместе с тем, она не способна значительно повысить качество диагностирования относительно эквивалентных одноуровневых моделей на основе LSTM-сетей. Время обучения рекуррентных нейронный сетей значительно превосходит время обучения сетей прямого распространения, а полученные результаты качества диагностирования схожи для рекуррентной и сети прямого распространения при использовании двухуровневой архитектуре, что позволяет говорить о целесообразности дальнейших исследований по анализу эффективности подобных архитектур устройств диагностирования.

Отдельно стоит выделить факт объединения диагнозов при классификации, т. е. использование только «сырых» данных датчиков в виде отрезков временных рядов ограничивает качество диагностирования. Необходим этап формирования диагностических признаков высших категорий – предобработки исходных данных для получения частотных, кепстральных и статистических представлений.

СПИСОК ЛИТЕРАТУРЫ

1. Hwang I., Kim S., Kim Y., Seah C.E. A survey of fault detection, isolation, and reconfiguration methods/ IEEE Trans. Control Syst. Technol., vol. 18, no. 3. Pp. 636-653.
2. Шестопалов М.Ю. Системы отказоустойчивого управления технологическими процессами. – СПб, Изд-во «Элмор», 2013. С. 308.
3. Шестопалов М.Ю., Имаев Д.Х. Диагностирование систем управления с помощью нейросетевых классификаторов распознавания неисправностей// Сб. докладов XVI Междунар. конф. по мягким вычисле-ниям и измерениям SCM-2013, Изд-во СПбГЭТУ «ЛЭТИ», 23-25 мая, т.1, 2013. С. 109 – 111.
4. Синица А.М., Викторов К.Д. Диагностирование неисправностей на базе LSTM нейронных сетей // Всероссийская научная конференция по проблемам управления в технических системах. 2017. № 1. С. 437-440.
5. Rowen WI. Simplified Mathematical Representations of Heavy-Duty Gas Turbines. ASME. J. Eng. Power. 1983;105(4):865-869. doi:10.1115/1.3227494
6. M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. J. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mane, R. Monga, S. Moore, D. G. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. A. Tucker, V. Vanhoucke, V. Vasudevan, F. B. Viegas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu, and X. Zheng. TensorFlow: Large-scale machine learning on heterogeneous distributed systems. // Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI ’16), Savannah, GA, USA, November 2–4, 2016

 

Уважаемые коллеги, если вы используете материалы статьи в своих работах просьба ссылаться на одну из следующих работ:

• Д. Х. Имаев, А. М. Синица, М. Ю. Шестопалов, С. В. Квашнин. Разработка нейросетевых моделей диагностирования систем управления турбоагрегатом // Международная научная конференция «IEEE Northwest Russia Conference On Mathematical Methods In Engineering And Technology: ММEТ NW 2018». Сборник докладов. Санкт-Петербург. 10 — 14 сентября 2018 г. СПб.: СПбГЭТУ «ЛЭТИ». С. 62-65
• Imaev D.Kh., Sinitca A.M., Shestopalov M.Yu., Kvashnin S.V. Development of Neural Network Diagnosing Models of Turbine Control Systems. // Proceedings of the 2018 IEEE Northwest Russia Conference on Mathematical Methods in Engineering and Technology (MMET NW). 10-14 September, 2018. St. Petersburg, Russia: Saint Petersburg Electrotechnical University “LETI”. 590 p., pp 72-75