Рассмотрим метод частотного синтеза корректирующих устройств основанный на анализе логарифмических амплитудных частотных характеристик (ЛАЧХ) и корректировке ее до желаемого вида [1]. В качестве примера объекта используется маятник на каретке.
Передаточная функция объекта по каналу «усилие на каретку-угол отклонения маятника»:
\[W(s) = {{-33S^2}\over{S^4-196s^2}}\]
или в факторизованном виде:
\[W(s)={{-33S^2}\over{S^2(S-14)(S+14)}}\]
Необходимым условием стабилизации неустойчивого объекта является охват обратной связью. В первую очередь создадим контур обратной связи, стабилизирующий маятник в верхнем положении, то есть перемещающий неусточивый полюс +14 передаточной функции. Обратим внимание на то, что коэффициент усиления объекта имеет отрицательное значение.
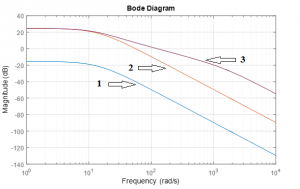
Построим ЛАЧХ объекта (рисунок 1). Как видно, усиление объекта (кривая 1) мало на частоте неустойчивого полюса.
Введем в контур усилитель с коэффициентом усиления 100, что поднимает ЛАЧХ на 40 дБ (кривая 2). Данная операция повысит быстродействие системы и обеспечит необходимую подвижность неустойчивого полюса.
Далее необходимо сформировать желаемый вид ЛАЧХ в области средних частот. Как известно, для устойчивости системы необходимо, чтобы асимптотическая ЛАЧХ контура на средних частотах имела наклон –20 дБ/дек. Для достижения цели ведем в контур действительный нуль z_1=-27 и действительный полюс p_1=-1500. Передаточная функция регулятора будет иметь вид
\[ W_{R1}(S) = 100 * {{1/27 S + 1}\over{1/1500S + 1}}\]
После построения частотной характеристики (рисунок 1, кривая 3), видим, что ЛАЧХ системы в окрестности частоты среза имеет наклон 20 дБ/дек.
Поскольку постоянная времени знаменателя много меньше постоянной времени числителя, можно полагать, что используется ПД-алгоритм регулирования.
Анализ замкнутой системы показывает, что собственные значения равны:
\[ \begin{bmatrix}0&0&-36&-97&-1367\end{bmatrix}\]
Значения являются отрицательными действительными, что говорит о значительном запасе устойчивости системы стабилизации маятника. Два нулевых собственных значения вызваны неустойчивостью положения каретки.
Для стабилизации положения каретки необходимо решать вторую часть задачи. Исходным объектом управления для синтеза второй подсистемы является система управления угловым положением маятника, синтезированная на первом этапе.
Вычислим передаточную функцию подсистемы, полученной на первом этапе, и представим ее в факторизованной форме:
\[ W_1 (s)={{10(s+1500)(s+5.716)(s-5.716)}\over{s^2 (s+1367)(s+97.47)(s+35.31))}} \]
Можно видеть, что передаточная функция является неминимально-фазовой ― имеет положительный нуль 5.716. Как известно, полюсы замкнутой системы стремятся к нулям разомкнутой системы, модули которых принадлежат диапазону частот с высоким усилением. Это свойство обязывает учитывать усиление на частоте положительного нуля: оно должно быть не выше значения –16…–20 дБ. При выполнении данного условия, замкнутая система не будет иметь собственных значений близких к положительному нулю объекта синтезированного на втором этапе.
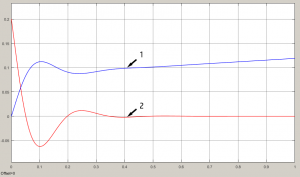
На рисунке 2 (кривая 1) показана ЛАЧХ системы, синтезированной на первом этапе, которая является объектом в задаче синтеза на втором этапе.
Чтобы достичь независимости контуров, т. е. их автономности, необходимо, чтобы ЛАЧХ второго контура имела малое усиление (меньше -16…-20 дБ) на частотах полюсов передаточной функции подсистемы, синтезированной на первом этапе. Для выполнения поставленных условий, замкнем вторую подсистему обратной связью с передаточной функцией регулятора:
\[ W_{R2} (s)={({1\over 0.15} s +1)\over({1\over 15} s + 1)} \]
что дает ЛАЧХ с отрезком асимптоты с наклоном -20 дБ/дек в окрестности частоты среза 0.7 рад/c. Поскольку постоянная времени знаменателя много меньше постоянной времени числителя, можно полагать, что во втором контуре также используется ПД-алгоритм регулирования.
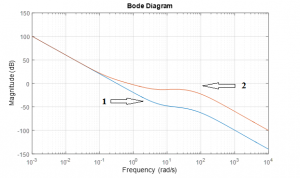
Стоит обратить внимание на то, что корректирующие устройства, синтезированные на первом и втором этапах, работают в области разных частот: низких и средних (рисунок 3), что говорит об автономности контуров.
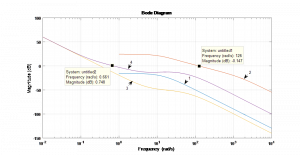
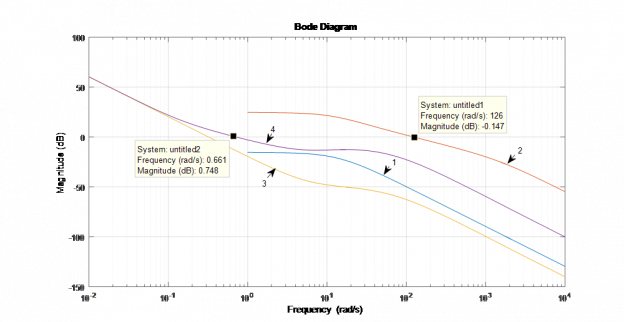
Рисунок 2.3 — ЛАЧХ: 1— исходного объекта; 2 — скорректированного исходного объекта; 3 — подсистемы, синтезированной на первом эта-пе; 4 — скорректированная система
Синтезированная система имеет следующие собственные значения:
\[ \begin{matrix}-1367\\-69+201j\\-69-201j\\-11\\-0.8\\-0.1\end{matrix} \]
Все собственные значения отрицательны, что говорит об успешном решении поставленной задачи синтеза ― обеспечении устойчивости «в малом» верхнего положения равновесия маятника.
Список литературы
- Душин С.Е., Зотов Н.С., Имаев Д.Х. и др. Теория автоматического управления: Учеб. для вузов; Под ред. В. Б. Яковлева.—М.: Высшая школа, 2003. — 567 с.: ил.
- Синица А.М. Разработка и исследование отказоустойчивой системы стабилизации маятника // Двадцатая Санкт-Петербургская Ассамблея молодых ученых и специалистов: Сборник тезисов — СПб.: Изд-во СПбГУПТД, 2015. — С. 144
- Минненбаев Р.М., Синица А.М. Стабилизация обратного маятника в положении устойчивого равновесия //Молодежная школа-семинар по проблемам управления в технических системах им. А.А. Вавилова: Сборник докладов. Санкт-Петербург. 28 октября 2016. СПб: Изд-во СПбГЭТУ “ЛЭТИ”. 2016 г. — с. 130

Уведомление: Оценка параметров ДУ в Python — Digiratory