В третий части цикла статей об автоколебаниях рассматриваются метод определения параметров периодических режимов Е.П. Попова.

Кроме этого метода известны еще, например, методы Л. С. Гольдфарба и А.А. Вавилова, но они являются графическими и, в силу развития вычислительной техники, не актуальны.

Метод Е.П. Попова

Метод гармонического баланса определения параметров автоколебаний, предложенный Е.П. Поповым основывается на критерии Гурвица.

Так как не ставится цель теоретического обоснования методов, наилучшим способом будет продемонстрировать алгоритм его применения.

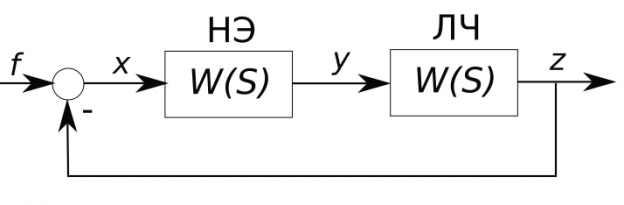
Рассмотри систему расчетной структуры, представленной ниже.

Примем, что нелинейный элемент имеет однозначную статическую характеристику. Как было показано ранее, в этом случае \(q’(A) = 0\), т.е. эквивалентная передаточная функция совпадает с коэффициентом гармонической линеаризации: \(W_n(A,S) = R_n(A) = q(A)\).

В случае в неоднозначными статическими характеристиками, эквивалентная передаточная функция, как говорилось ранее, принимает вид:

\[ W_n(A,S) = q(A)+\frac S{\omega} q’(A) \]

Передаточная функция линейной части может быть записана в следующем виде:

\[ W(S) = \frac{B(S)}{D(S)}\]

тогда выражение для характеристического полинома замкнутой гармонически линеаризованной системы получается в виде суммы:

\[ D_c(S, A) = D(S) + W_n(A,S) B(S) \]

Так как гармонически линеаризованная система, чтобы выполнялось условие наличия автоколебаний, должна находиться на границе устойчивости, то в соответствии с критерием Гурвица предпоследний определитель матрицы Гурвица должен равняться нулю (остальные определители должны быть положительны):

\[ \delta_{n-1}(A) = 0\]

Из этого условия вычисляется значение \(A^*\), которое подставляется в полином \(D_c\), имеющий пару мнимых корней (остальные левые):

\[ D_c(j \omega, A^*) = 0\]

Разделяя вещественную и мнимую часть, получаем два уравнения:

\[ Re D_c(j \omega, A^*) = 0\]

\[ Im D_c(j \omega, A^*) = 0\]

Искомая частота \(\omega^*\) получается решением любого из них.

Пример

Рассмотрим нелинейную систему, в которой нелинейный элемент — идеальное реле, а линейная часть имеет передаточную функцию:

\[ W(S) = \frac 1{S(S+1)^2}\]

Шаг 1. Получение коэффициента гармонической линеаризации

Коэффициенты получаются методом, описанным ранее или из справочных данных для типовых нелинейностей. Коэффициент гармонической реализации для идеального реле известен:

\[ q(A) = \frac{4C}{\pi A}\]

Шаг 2. Характеристический полином замкнутой системы

Как сказано ранее, характеристический полном вычисляется по формуле:

\[ D_c(S, A) = D(S) + W_n(A,S) B(S) \]

подставляя в нее исходные данные получаем:

\[ D_c(S, A) = S(S+1)^2 +\frac{4C}{\pi A}=S^3 + 2S^2 + S +\frac{4C}{\pi A} \]

Шаг 3. Условием колебательной границы устойчивости

Условием колебательной границы устойчивости для полинома третьего порядка является равенство произведений средних и крайних коэффициентов:

\[ 2 * 1 = 1 *\frac{4C}{\pi A} \]

из чего следует \(A^* = {2C}/{\pi}\). При подстановке этого выражения в \(D_c(S, A)\) получаем:

\[ D_c(j \omega, A^*)  = -j \omega^3 – 2 \omega^2 + j \omega + 2 = 0\]

или

\[ Re D_c(j \omega, A^*) = -2\omega^2 + 2 = 0 \]

\[ Im D_c(j \omega, A^*) = \omega -\omega^3 = 0\]

Решая уравнение, получаем частоту \(\omega^* = 1 c^{-1}\) периодического режима. Второе уравнение имеет два корня: \(\omega^*_1 = 1; \omega^*_2 = 0 \), второй корень не принимается во внимание.

Источник

• Теория автоматического управления: Учеб. для вузов/С.Е. Душин, Н.С. Зотов, Д.Х. Имаев и др.; Под ред. В.Б. Яковлева. — М.: Высшая школа, 2003. — 567 с.

Оглавление

1. Автоколебания. Введение
2. Автоколебания. Гармоническая линеаризация
3. Автоколебания. Определение параметров периодических режимов
4. Автоколебания. Устойчивость