Одной из распространенных задач, возникающих при исследовании различных объектов — построение математической модели. Нередко математическая модель представляется в виде системы дифференциальных уравнений, однако непосредственное измерение всех, входящих в них параметров, как правило, невозможно по различным причинам. В таком случае, одним из подходов является проведение идентификационных экспериментов и оценка параметров ДУ путем решения оптимизационной задачи.
В статье рассмотрен простой способ оценки параметров системы ДУ в форме Коши на языке Python.
Постановка задачи
Разработка простого модуля Python для решения задачи оценки параметров.
Исходные данные для задачи:
- Представление модели в форме Коши, первые N величин — наблюдаемы (порядок уравнений не имеет значения с точки зрения математики, но упорядочивание сильно упростит жизнь при разработке);
- Имеются данные эксперимента, на основе которого будет производится оценка параметров/
Исходные данные
Исходными данными, передаваемыми при создании экземпляра класса оценки параметров являются:
- Функция, реализующая вычисление ДУ.
- Массив экспериментальных данных (Два массива: время и значения)
Таким образом, получаем следующий класс с конструктором:
class parameter_estimator():
def __init__(self, x_data, y_data, f):
self._x_data = x_data
self._y_data = y_data
self._f = f
self._c = None
self.n_observed = y_data.shape[1]
Тут просто сохраняются значения параметров и функция в поля класса.
Оценка параметров
Процедуру оценки параметров можно сделать на основе функции scipy.optimize.leastsq. Эта функция минимизирует сумму квадратов полученных величин и может принимать два интересных для начального понимания аргумента: func и x0.
Функция func должна принимать один аргумент (который м.б. вектором), являющийся параметрами, а x0 — начальные значения параметров.
Метод оценки параметров можно реализовать следующим образом:
def estimate(self, y0, guess):
"""
Произвести оценку параметров дифференциального уравнения с заданными
начальными значениями параметров:
y0 -- начальные условия ДУ
guess -- параметры ДУ
"""
# Сохраняем число начальных условий
self._y0_len = len(y0)
# Создаем вектор оцениваемых параметров,
# включающий в себя начальные условия
self._est_values = np.concatenate((y0, guess))
# Решить оптимизационную задачу - решение в переменной c
(c, kvg) = optimize.leastsq(self.f_resid, self._est_values)
self._c = c
# В возвращаемом значении разделяем начальные условия и параметры
return c[self._y0_len:], c[0:self._y0_len]
Метод получает начальные значения начальных условий ДУ и начальные значения параметров системы. Функцию вычисления вектора ошибок между решением системы ДУ с текущими значениями параметров и экспериментальными значениями необходимо реализовывать самостоятельно, потому, следующим шагом будет ее написание:
def f_resid(self, p):
"""
Функция для передачи в optimize.leastsq
При дальнейших вычислениях значения, возвращаемые этой функцией,
будут возведены в квадрат и просуммированы
"""
delta = self._y_data - self.my_ls_func(self._x_data, p)
return delta.flatten() # Преобразуем в одномерный массив
Функция получает вектор параметров системы (включая начальные условия ДУ).
Предложенная функция содержит вызов еще одной функции my_ls_func, выделенной для разделения функционала. Выглядит она следующим образом и вычисляет непосредственно решение системы ДУ при заданных параметрах:
def my_ls_func(self, x, teta):
"""
Определение функции, возвращающей значения решения ДУ в
процессе оценки параметров
x заданные (временные) точки, где известно решение
(экспериментальные данные)
teta -- массив с текущим значением оцениваемых параметров.
Первые self._y0_len элементов -- начальные условия,
остальные -- параметры ДУ
"""
# Для передачи функции создадим ламбда-выражение с подставленными
# параметрами
# Вычислим значения дифференциального уравнения в точках "x"
r = integrate.odeint(lambda y, t: self._f(y, t, teta[self._y0_len:]),
teta[0:self._y0_len], x)
# Возвращаем только наблюдаемые переменные
return r[:, 0:self.n_observed]
Таким образом, процедура оценки параметров работает следующим образом:
- Вычисляется решение системы ДУ при текущих (или начальных) значения параметров.
- Рассчитывается вектор ошибки между решением и экспериментальными данными.
- Производится корректировка значений параметров.
- Переход на шаг 1, если не достигнуто максимальное число итераций или минимальное рассогласование.
Визуализация
Для визуализации напишем следующую функцию:
def plot_result(self):
"""
Построить графическое представление результатов оценки параметров
"""
if self._c is None:
print("Parameter is not estimated.")
return
sol, t = self.calcODE((self._c[self._y0_len:],),
self._c[0:self._y0_len],
min(self._x_data),
max(self._x_data))
# Строим экспериментальные данные, как красные точки,
# а результаты моделирования, как синюю линию
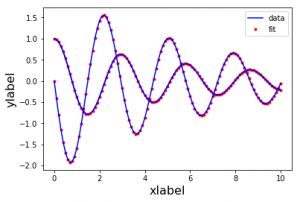
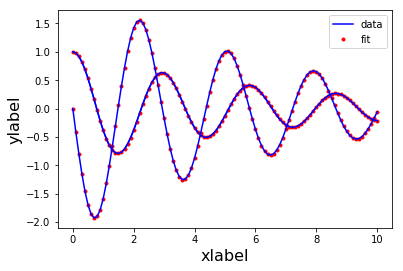
pp.plot(self._x_data, self._y_data, '.r', t, sol, '-b')
pp.xlabel('xlabel', {"fontsize": 16})
pp.ylabel("ylabel", {"fontsize": 16})
pp.legend(('data', 'fit'), loc=0)
pp.show()
где calcODE — еще одна служебная функция для расчета системы ДУ:
def calcODE(self, args, y0, x0=0, xEnd=10, nt=101):
"""
Служебная функция для решения ДУ
"""
t = np.linspace(x0, xEnd, nt)
sol = odeint(self._f, y0, t, args)
return sol, t
Тестирование и пример использования
В качестве примера использования попробуем оценить параметры системы ДУ, описывающие маятник с трением.
\[ {d \theta \over dt } = \omega \\ {d \omega \over dt } = -b * \omega — c* \sin(\theta) \]
где \(\theta \) — угол, \(\omega\) — скорость.
Этот объект уже использовался в качестве иллюстрации к статье о фазовых портретах и частотному методу синтеза регуляторов.
Для получения «экспериментальных» данных воспользуемся решением системы ДУ с известными «истинными» параметрами:
def ode(y, t, k):
"""
Функция, реализующая систему ДУ маятника с трением
"""
theta, omega = y
b = k[0]
c = k[1]
dydt = [omega, -b*omega - c*np.sin(theta)]
return dydt
def calcODE(args, y0, dy0, ts=10, nt=101):
"""
Вспомогательная функция для получения решения систему ДУ
"""
y0 = [y0, dy0]
t = np.linspace(0, ts, nt)
sol = odeint(ode, y0, t, args)
return sol, t
# Зададим истинные значения параметров системы
b = 0.3
c = 5.0
args = ([b, c], )
y0 = 1
dy0 = 0
print("Real parameter: b = {}, c = {}".format(b, c))
print("Real initial condition: {} {}".format(y0, dy0))
sol, t = calcODE(args, y0, dy0)
Объявленная тут система будет использоваться и для оценки параметров, но уже без известных значений:
# Зададим истинные значения параметров системы
b = 0.3
c = 5.0
args = ([b, c], )
y0 = 1
dy0 = 0
print("Real parameter: b = {}, c = {}".format(b, c))
print("Real initial condition: {} {}".format(y0, dy0))
sol, t = calcODE(args, y0, dy0)
guess = [0.2, 0.3] # Начальные значения для параметров системы
y0 = [0, 1] # Стартовые начальные значения для системы ДУ
estimator = parameter_estimator(t, sol, ode)
est_par = estimator.estimate(y0, guess)
# Построим графики результатов оценки параметров
estimator.plot_result()
print("Estimated parameter: b={}, c={}".format(est_par[0][0], est_par[0][1]))
print("Estimated initial condition: {}".format(est_par[1]))
Получившиеся результаты являются достаточно точно оценкой:
Real parameter: b = 0.3, c = 5.0
Real initial condition: 1 0
Estimated parameter: b = 0.299993833612628, c = 5.000066486504925
Estimated initial condition: [ 9.99976783e-01 1.58491793e-04]