В заметке рассмотрим пример, как можно быстро настроить локального ассистента на базе большой языковой модели (LLM) для написания код в Visual Studio Code.
Читать далее
Архив рубрики: manual
Сверточные нейронные сети для компьютерного зрения [0.4] Инструкция по использованию Google Cloud
Для проектов и задач данного курса, авторы предлагают использовать Google Compute Engine для разработки и тестирования ваших реализаций, однако, по нашему мнению это не самый лучший вариант. В этом руководстве перечислены необходимые шаги для работы над заданиями с помощью Google Cloud. Мы рассчитываем, что изучение этого руководства займет около 1 часа. Не пугайтесь шагов, мы постарались сделать это руководство наиболее подробным, чтобы у вас было меньше шансов застрять на определенном шаге.
Это руководство говорит о том, как настроить собственный экземпляр Google Compute Engine (GCE) для работы с заданиями. После первой регистрации, вы по умолчанию получите $300 от Google.
Читать далее
Сверточные нейронные сети для компьютерного зрения [0.2] Инструкция по использованию Python/Numpy
Оригинал инструкции был составлен Джастином Джонсоном.
Мы будем использовать язык программирования Python для всех заданий этого курса. Python это отличный универсальный язык программирования сам по себе, но с помощью некоторых популярных библиотек (numpy, scipy, matplotlib) он становиться мощным окружением для научных вычислений.
Несмотря на предположение, что читатель имеет некоторый опыт использования Python и numpy, для этот раздел послужит быстрым вводным курсом по языку программирования Python и использовании Python для научных вычислений для читателей с недостаточными навыками.
Читать далееПостроение одномерных (Одна переменная, один параметр) бифуркационных диаграмм в Maxima
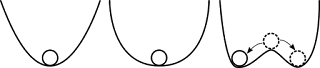
Слов «бифуркация» означает «раздвоение» и употребляет как название любого скачкообразного изменения, происходящего при плавном изменении параметров в любо системе: динамической, экологической и т. д.
Бифуркации имеют фундаментальное значение при исследовании поведения динамических систем. Часто именно бифуркации определяют механизм возникновения многих сложных процессов.
Рассмотрим способ построения бифуркационных диаграмм для простейших систем с помощью Maxima
В математике, особенно при изучении динамических систем, под понятием бифуркационная диаграмма подразумевают изображение на рисунке смены возможных динамических режимов системы (равновесных состояний, стационарных точек, периодических орбит и пр.) при изменении значения бифуркационного параметра. [Википедия].
Таким образом на диаграмме отражена динамика изменения положений равновесия в зависимости от изменения некого параметра системы.
Построение диаграммы рассмотрим на примере седло-узловой бифуркации в системе, описываемой д.у.
где λ — варьируемый параметр (В среде Maxima будем использовать L). Необходимо определить равновесные решения. Для этого воспользуемся командой
b4_1: solve(L-x^2=0, x);
(b4_1)[x=-sqrt(L),x=sqrt(L)]
Теперь для построения диаграммы воспользуемся командой:
plot2d( [ rhs(b4_1[1]),rhs(b4_1[2]) ], [ L, -5, 5 ], [ xlabel, «L» ], [ ylabel, «Точки равновесия» ],[legend, false] );
Получим следующий результат:
Получим следующий результат:
Бифуркационная диаграмма
Как видно из рисунка, из точки бифуркации выходят две ветви равновесных состояний, одна из которых устойчивая, а вторая — неустойчивая. При варьировании параметра в сторону увеличения значений из «ничего» рождаются два состояния равновесия, одно из которых устойчиво. Бифуркации такого рода относят к типу «седло-узел».
plot2d() — построение двумерного графика
rhs() — получение правой части равенства, в нашем случае функции x(L)
[ xlabel, «L» ] — Задаем название оси X
[ ylabel, «Точки равновесия» ] — Задаем название оси Y
[legend, false] — отключаем легенду
Аналогичным образом можно построить диаграмц и для системы с большим числом решений/
Больше информации о бифуркациях и больше примеров ищите на digiratory.ru