Теория бифуркаций проявляется повсеместно в естествознании. Дифференциальные уравнения, описывающие реальные физические системы, всегда содержат параметры, точные значения которых, не известны. Если уравнение, моделирующее физическую систему, оказывается структурно неустойчивым, то есть поведении его решении может качественно измениться при сколь угодно малом изменении правой части, то необходимо определить, какие бифуркации фазового портрета происходят при изменении параметров

Весьма важным и продуктивным понятием естествознания является понятие динамической системы. Под динамической системой понимают математическую модель того или иного реального процесса, обладающую следующими свойствами. Во-первых, должен быть известен некоторый набор величин, который однозначно задает состояние системы. Во-вторых, должен быть известен закон, по которому можно однозначно определить состояние системы в любой момент времени, если известно ее начальное состояние. Это понятие является очень широким и поэтому примеры динамических систем можно найти практически во всех областях физики, биологии, химии и т.д.

Поведение динамической системы, в частности, установившиеся с течением времени режимы, могут зависеть от некоторых параметров. Оказывается, что при медленном изменении параметра могут происходить качественные перестройки установившихся режимов. Изучение таких перестроек при вариации параметров в динамических системах (причем, не только в отображениях, но и в дифференциальных уравнениях) составляет предмет теории бифуркаций. Она выявляет типичные бифуркации, изучает и классифицирует их. Теория бифуркаций является математической наукой.

Слово «бифуркация» означает «раздвоение» и употребляет как название любого скачкообразного изменения, происходящего при плавном изменении параметров в любо системе: динамической, экологической и т. д. Статья посвящена бифуркациям нелинейных динамических систем.

Часто при моделировании физических процессов часть переменных, изменения которых незначительны в рамках моделируемых процессов, принимают константами. В результате получается система более низкого порядка, чем исходная, но учесть влияние изменения членов, принятых за постоянные, становится невозможно. В этом случае члены можно рассматривать, как возмущения и описывать модель средствами теории бифуркаций.

Бифуркации допускают определенную классификацию. Во-первых, по минимальной величине размерности системы, для которой возможна данная бифуркация. А, во-вторых, по минимальному количеству параметров, необходимых для данного типа перестройки.

1. Понятие бифуркации

Бифуркации имеют фундаментальное значение при исследовании поведения динамических систем. Часто именно бифуркации определяют механизм возникновения многих сложных процессов. Остановимся на некоторых основных положениях теории бифуркации.

Пусть нелинейная модель автономной системы, представленная ДУ

\begin{equation} {dx \over dt} = F(x,\lambda) \end{equation}

характеризуется изменением параметра \( \lambda\). В реальной системе таким параметром может быть температура, давление, концентрация, коэффициент роста популяции и т. д. Следует подчеркнуть, что изучению подлежит не конкретная модель с фиксированным параметром, а семейство динамических моделей, поведение которых зависит от \(\lambda\).

При некотором значении параметра, называемым критическим значением, процессы в системе претерпевают качественное изменение. В этом случае структура (топология) разбиения фазового пространства (фазовой плоскости при размерности 2) на траектории также качественно изменяется. Такое свойство нелинейной системы принято называть бифуркацией (от латинского слова bifurcus – раздвоенный), а варьируемый параметр \(\lambda\), при котором наблюдается бифуркация – бифуркационным параметром.

Более строго, бифуркационным (критическим) значением параметра \(\lambda\) называется такое его значение, при котором динамическая система становится негрубой (структурно-неустойчивой).

Понятие грубости динамической системы было введено А.А. Андроновым и Л.С. Понтрягиным. Динамическая система, представленная ДУ следующего вида

\[{dx_i \over dt} = F(x), x = 1, …, n \]

называется грубой в области \(G \subset {{\bf{R}}^n}\), если для любого \(\varepsilon  > 0\) можно указать такое \(\delta  > 0\), что при произвольных аналитических функциях \({Q_i}({x_1},\; \ldots ,\;{x_n}) = {Q_i}({\bf{x}})\) изменённой (другими словами – возмущённой) системы

\[\frac{{d{x_i}}}{{dt}} = {F_i}({\bf{x}}) + {Q_i}({\bf{x}}),i = 1,\; \ldots ,\;n\]

удовлетворяющих неравенству

\[\sum\limits_{i = 1}^n {\left[ {\left| {{Q_i}({\bf{x}})} \right| + \sum\limits_{j = 1}^n {\left| {\frac{{\partial {Q_i}({\bf{x}})}}{{\partial {x_j}}}} \right|} } \right] < \delta } \]

существует такое взаимно однозначное и взаимно непрерывное отображение области в себя, при котором каждая траектория исходной (невозмущённой) системы отображается в соответствующую траекторию системы и обратно. При этом соответствующие друг другу точки находятся на расстоянии, меньшем \(\varepsilon \). Другими словами, грубыми являются такие динамические системы, у которых качественная структура фазовых траекторий не меняется при произвольном малом изменении правых частей исходного ДУ.

Для грубых динамических систем второго порядка выполняются следующие условия:

1. в области \(G \subset {{\bf{R}}^2} \)могут располагаться только простые особые точки (состояния равновесия) типа «узел», «фокус», «седло», т. е. такие, для которых действительные части корней характеристического уравнения линеаризованной системы отличны от нуля. Такие особые точки (их конечное число) называются грубыми;
2. в области \(G\) могут располагаться только простые предельные циклы, число которых конечно;
3. в области \(G\) отсутствуют сепаратрисы, идущие из седла в седло. Возможно существование сепаратрис сёдел, в одну сторону стремящиеся к узлу, фокусу, предельному циклу или при некотором значении \(t\) выходящие из области \(G\).

При нарушении этих условий динамическая система становится негрубой.

В соответствии с теорией бифуркаций в пространстве координат и параметра из точки бифуркации могут исходить несколько ветвей решения уравнения равновесия

\[{\bf{0}} = {\bf{F}}({\bf{x}},\;\lambda )\]

как устойчивых, так и неустойчивых. Графики зависимости координат положений равновесия от \(\lambda\) представляют собой бифуркационные диаграммы.

Простейшим примером бифуркации может служить следующая система

\[\frac{{dx}}{{dt}} = \lambda x\]

которая имеет решение \(x(t) = {x_0}{e^{\lambda t}}\), определяющее экспоненциальный рост (убывание), если \(\lambda  > 0(\lambda  < 0)\) соответственно. Заметим, что приведенное выше уравнение определяет динамику цепной реакции \(\lambda  > 0\) и распада ядра \(\lambda  < 0\). Единственное состояние равновесия уравнения \(x = 0\) устойчиво при \(\lambda  < 0\) и неустойчиво при \(\lambda  > 0\).

Рис. 1.1 — Временная характеристика системы при различных значениях бифуркационного параметра

2. Классификация

Бифуркации принято классифицировать по числу нарушений условий гиперболичности собственных значений матрицы

\[{\bf{J}}({\bf{x}},\;{\lambda _1},\; \ldots ,\;{\lambda _m}) = \left\| {\frac{{\partial {F_i}({\bf{x}},\;{\lambda _1},\; \ldots ,\;{\lambda _m})}}{{\partial {x_j}}}} \right\|\]

Неподвижная точка называется гиперболической, если матрица Якоби \({\bf{J}}\), определённая в ней, не содержит собственных значений \({s_k} \) с нулевой действительной частью, т. е. \({\rm{Re}}\,{s_k} \ne 0\).

При рассмотрении многопараметрического пространства \(\Lambda \) точка этого пространства (\(\lambda \in \Lambda \)), в которой происходит качественное изменение поведения динамической системы, именуется точкой бифуркации. Для пространства \(\Lambda \) характерна задача определения числа параметров \(\{ {\lambda _q}\} \), которые должны присутствовать в модели для того, чтобы данная бифуркация относилась к типичной.

Собственные значения \({s_k} \) матрицы \({\bf{J}}\) представляют собой функции от параметров, т. е. \({s_k}({\lambda _1},\; \ldots ,\;{\lambda _m})\). Тогда условия нарушения гиперболичности вида \({\rm{Re}}\,{s_k} = 0\) определяются системой уравнений, составленных относительно параметров. Например, для того, чтобы два действительных собственных значения одновременно обратились в ноль, необходимо найти решение системы двух уравнений относительно неизвестных

\[\begin{array}{l}
{s_1}({\lambda _1},\; \ldots ,\;{\lambda _m}) = 0\\
{s_2}({\lambda _1},\; \ldots ,\;{\lambda _m}) = 0
\end{array}\]

При этом возможны следующие типичные ситуации:

• если \(m = 1 \) , то решение в общем случае отсутствует; бифуркация не обнаруживается;
• если \(m = 2 \), то возможно решение; бифуркация может произойти в одной или нескольких точках \(\Lambda \);
• если \(m > 2 \), то в типичных случаях негиперболические точки будут располагаться на поверхности размерности \(m — 2 \) в \(\Lambda \) , т. е. могут образовываться поверхности бифуркации.

В общем случае, если необходимо удовлетворить \(k \) условиям нарушения гиперболичности, то возможные точки бифуркации будут располагаться на \((m — k)\) -мерной поверхности. Величину \(k \), определяющую количество условий нарушения гиперболичности, называют коразмерностью бифуркации. Разность между размерностью пространства и размерностью поверхности бифуркации представляет собой коразмерность поверхности.

Коразмерность бифуркации показывает, каким числом параметров должна определяться динамическая система, чтобы наблюдаемая в ней бифуркация была типичная. Другими словами, коразмерность бифуркации – наименьшая размерность пространства \(\Lambda \), в котором возможна бифуркация соответствующего типа. В дальнейшем для простоты понимания основных положений теории бифуркаций целесообразно ограничиться рассмотрением бифуркаций коразмерности 1, которые наблюдаются в однопараметрических системах. С бифуркациями более высокого порядка можно ознакомиться в специальной литературе.

Изучение распространённых типов бифуркаций производится на моделях первого и второго порядков, представленных определёнными ДУ. При этом в линеаризованных моделях возникает одно нулевое или два мнимых собственных значений матрицы Якоби.

2.1 Бифуркации в системах с простым движением

Негрубость системы означает негрубость тех или иных траекторий. Среди таких траекторий прежде всего выделяются устойчивые состояния равновесия и периодические движения, поскольку они являются математическим образом стационарных состояний и автоколебаний.

Состояние равновесия n-мерной системы \(\mathop x\limits^. = X(x)\) точка \(M({x^*})\), где \({x^*}\) — решение системы \(X(x) = 0\). Оно негрубое, если среди \({\lambda _{1,}}{\lambda _2}, …{\lambda _n}\) — корней характеристического уравнения \(\det (\frac{{\partial X({x^*})}}{{\partial x}} — \lambda E) = 0\) имеются корни, лежащие на мнимой оси. В случае, если \({\mathop{\rm Re}\nolimits} {\lambda _i} < 0,i = 1,…n \), состояние равновесия является устойчивым. Если имеются корни как с отрицательной, так и с положительной реальной частью, то состояние равновесия носит название седлового. К нему будут стремиться траектории как при \(t \to  + \infty \), так и при \(t \to  — \infty \) , в совокупности образуя устойчивое \({W^s}\) и неустойчивое \({W^u}\) многообразия. Периодическое решение \(x = \phi (t) \) этой системы будет негрубым, если среди мультипликаторов \({\rho _1},{\rho _2},…{\rho _{n — 1}}\) имеются равные по модулю 1. Если же \(\left| {{\rho _i}} \right| < 1\), периодическое движение устойчивое, и седловое, если среди мультипликаторов есть как лежащие внутри единичного круга, так и вне его.

В настоящее время основные (коразмерности 1) локальные и глобальные бифуркации таких траекторий подробно изучены.

Устойчивое состояние равновесия может:

1. исчезнуть, слившись с неустойчивым. В момент бифуркации у состояния равновесия, называемого седло-узел, только один характеристический корень лежит на мнимой оси и равен нулю.
2. потерять устойчивость. При этом из состояния равновесия будет рождаться (влипать в него) устойчивое (неустойчивое) периодическое движение, если в момент бифуркации состояние равновесия устойчиво (неустойчиво). Эта бифуркация, объясняющая генерацию колебаний, носит название Андронова-Хопфа.

Устойчивое периодическое движение может:

• исчезнуть, слившись с неустойчивым в момент бифуркации. Для \(n > 2\) негрубое периодическое движение носит название седло-узлового.
• потерять устойчивость с рождением устойчивого
  • периодического движения удвоенного периода, если мультипликатор равен (-1),
  • двумерного инвариантного тора, если \({\rho _{1,2}} = {e^{ \pm i\phi }}\), где \(\phi  \ne 0,\pi ,\frac{\pi }{2},\frac{{2\pi }}{3}\).

Устойчивые периодические движения могут также рождаться в результате следующих глобальных бифуркаций:

1. из траектории, идущей из седла с характеристическими корнями \({\mathop{\rm Re}\nolimits} {\lambda _i} < 0\), \(i=1, … ,n-1\), и седловой величиной \( \max {\mathop{\rm Re}\nolimits} {\lambda _i} + {\lambda _n} < 0\)  в то же седло,
2. из траектории, идущей из седло-узла в него при исчезновении состояния равновесия,
3. при исчезновении седло-узлового периодического движения, все траектории неустойчивого многообразия которого, образуют в совокупности сильно сжимающуюся трубку, навивающуюся на периодическое движение. Эта бифуркация называется «катастрофой голубого неба» и ее особенность состоит в том, что при стремлении параметра к бифуркационному значению длина периодических движений стремится к бесконечности.

В случае коразмерности 1 седловые периодические движения могут рождаться из траектории, идущей 1) из седла в него же, 2) из негрубого состояния равновесия типа седло-седло в него же при его исчезновении (такое состояние равновесия образуется при слиянии двух грубых седел.)

Все перечисленные бифуркации не выводят из класса систем с простым поведением траекторий.

2.2 Бифуркации в системах со сложным движением

Основным признаком системы со сложным поведением траекторий является существование грубого предельного множества, состоящего из траекторий седлового типа, в котором всюду плотны постоянные движения и есть всюду плотная траектория. Такие множества называются гиперболическими. Наиболее универсальный критерий существования таких множеств связан с гомоклинической орбитой Пуанкаре — двояко асимптотической траекторией к седловому постоянному движению, по которой его устойчивое и неустойчивое многообразия пересекаются без касания. Наличие такой структуры гарантирует существование в любой ее малой окрестности одномерного гиперболического множества, но неустойчивого. По этой причине бифуркации, связанные с появлением или исчезновением гиперболического множества, получили общее название гомоклинических. Другим типичным случаем систем со сложным поведением траекторий являются системы с гомоклиническими петлями седло-фокуса с положительной седловой величиной. Гомоклинические бифуркации подразделяются на два типа: граничные, объясняющие переходы от простой динамики к сложной, и внутренние. Характерным примером бифуркации 1-го типа, показывающим, что системы с простой и сложной динамикой могут быть разделены бифуркационной поверхностью, является бифуркацией исчезновения состояния равновесия типа седло-седло с не менее, чем двумя двояко асимптотическими траекториями, а также ряд бифуркаций систем с негрубой гомоклинической траекторией Пуанкаре. Однако такому переходу может предшествовать бесконечный каскад бифуркаций удвоения периода Шарковского-Фейгенбаума. Отметим также задачу о разрушении тора в связи с проблемой синхронизации.

В случае внутренних бифуркаций одной из основных задач является выделение в пространстве динамических систем областей негрубых систем. Впервые на это необычное явление было указано Смейлом в начале 60-х годов. Но наибольшую известность получили области Ньюхауса, в которых всюду плотны системы с негрубыми гомоклиническими траекториями Пуанкаре, имеющие постоянного движения любого порядка вырождения. Из этого следует вывод — для нелинейной динамики: полный качественный анализ моделей, допускающих негрубую гомоклиническую траекторию Пуанкаре, не реалистичен.

С открытием динамического хаоса в теории бифуркаций открылась новая глава, связанная с теорией странных аттракторов – притягивающих предельных множеств с неустойчивым поведением траекторий. В отличие, например, от постоянных движений, странные аттракторы не имеют унифицированной природы: они могут быть как многообразием (гладким или негладким), так и множествами с весьма сложной теоретико-множественной структурой. Исходя из интересов нелинейной динамики, от странных аттракторов требуется, чтобы они сохраняли свои свойства при малых возмущениях системы. Естественно, это так для гиперболических аттракторов. Но анализ ряда моделей показал, что таковыми могут быть и негрубые аттракторы. Характерным примером является странный аттрактор модели Лоренца \( \mathop x\limits^. = — \sigma (x — y),\mathop y\limits^. = — y + rx — xz,\mathop z\limits^. = — bz + xy\), негрубость которого обусловлена тем, что состояние равновесия типа седло принадлежит странному аттрактору. В размерности n>3 могут быть негрубые аттракторы, содержащие седло-фокус. Поскольку последние допускают гомоклинические касания, их (по выше приведенным причинам) принято называть «дикими». Понятно, что изучение бифуркаций, приводящих к возникновению странных аттракторов, стало одной из актуальных задач. Исторически эта проблема возникла в гидродинамике в связи с объяснением возникновения турбулентности. Именно в этой связи в 40-х годах Ландау и Хопф предложили такое объяснение на примере каскада бифуркаций торов с повышением их размерности. Гидродинамическое происхождение имеет и модель Лоренца. Здесь переход от простой динамики к странному аттрактору происходит в результате двух гомоклинических бифуркаций: граничной бифуркации гомоклинической восьмерки-бабочки седла, в результате которой рождается неустойчивое одномерное гиперболическое множество, и внутренней бифуркацией гомоклинического контура в момент, когда обе траектории, выходящие из седла, впервые устремятся к седловым постоянным движением, появившимся в результате граничной бифуркации. Однако такой, сравнительно простой сценарий, обусловлен тем, что модель Лоренца обладает симметрией \(( — x, — y) \to (x,y)\). Отметим также следующий результат, имеющий пока чисто математическое значение, — ряд гиперболических аттракторов (соленоид Смейла-Вильямса, аносовский тор), могут рождаться в результате глобальных бифуркаций, связанных с исчезновением седло-узловых постоянных движенй и торов. Помимо странных аттракторов во многих прикладных исследованиях встречаются предельные множества, которые можно назвать квазиаттракторами, поскольку в них, кроме гиперболических множеств, содержатся устойчивые постоянные движения, причем даже в счетном множестве. Подобная ситуация возникает, например, в трехмерных системах с отрицательной дивергенцией. В компьютерных исследованиях динамика модели в областях Ньюхауса может вполне ассоциироваться с хаотическим поведением траекторий, поскольку п.д. могут иметь весьма большие периоды и узкие области притяжения.

3. Мягкая и жесткая потеря устойчивости

3.1 Понятие мягкой и жесткой потери устойчивости

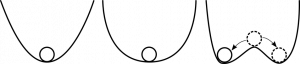
Бифуркации условно можно разделить на мягкие и жёсткие, что наглядно демонстрируется следующим примером. На рис. 3.1 и рис. 3.2 изображён перестраиваемый профиль с шариком. В результате изменения какого-либо фактора (параметра), исходный профиль изменяет свою конфигурацию таким образом, что устойчивое равновесное состояние шарика теряется. При этом «рождаются» два новых устойчивых состояния равновесия, в один из которых и сваливается шарик. Вновь появившиеся состояния равновесия перестроившегося профиля располагаются в непосредственной близости от начального состояния равновесия, которое потеряло устойчивость. Бифуркации такого типа называют мягкими. Новый режим функционирования как бы постепенно появляется из режима, потерявшего устойчивость, и сосуществует рядом с ним.

Рис. 3.1 — перестраиваемый профиль с шариком

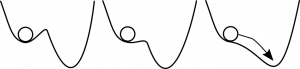
Характер перестроения профиля, изображённого на рис. 3.2, иной. Для значения параметра меньше критического шарик находится в устойчивом равновесном состоянии. Одновременно существует ещё одно потенциальное неустойчивое равновесное состояние. При перестроении профиля для критического значения параметра устойчивое и неустойчивое состояния сливаются в одно. Далее они оба исчезают, и система «скачком» выбирает новый режим, который существенно отличается от предыдущего и не находится в непосредственной близости от исходного режима. Бифуркации такого типа относятся к жёстким. Именно жёсткие (скачкообразные) бифуркации в первую очередь являются предметом исследования теории катастроф.

Рис. 3.2 — перестраиваемый профиль с шариком

4. Виды бифуркаций

В следующем разделе будут описаны основные виды и примеры бифуркаций как непрерывных, так и дискретных (отражений) функций.

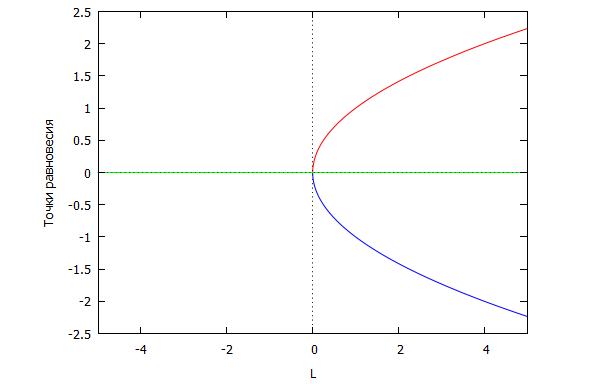
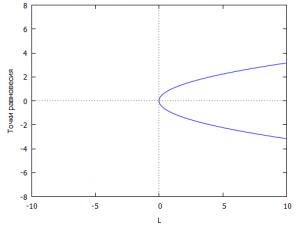
4.1 Касательная (седло-узловая) бифуркация

Пример седло-узловой бифуркации рассмотрим на примере системы, описываемой д.у.:

\[\frac{{dx}}{{dt}} = \lambda  — {x^2}\]

где \(\lambda \) — варьируемый параметр. Равновесные решения \(x_{{\rm{1}}{\rm{,2}}}^{\rm{}} =  \pm \sqrt \lambda  \) уравнения определены только для \(\lambda  \ge 0\); при \(\lambda  < 0\) равновесные состояния отсутствуют. Значение \(\lambda  = 0\) является бифуркационным. На рис. 4.2 изображена соответствующая бифуркационная диаграмма. Как видно из рисунка, из точки бифуркации \((x = 0,\;\lambda  = 0)\) выходят две ветви равновесных состояний, одна из которых устойчивая, а вторая — неустойчивая. При варьировании параметра в сторону увеличения значений из «ничего» рождаются два состояния равновесия, одно из которых устойчиво. Бифуркации такого рода относят к типу «седло-узел».

Рис. 4.1 — Временная характеристика системы с касательной (седло-узловой) бифуркацией

Рис 4.2 — Диаграмма касательной (седло-узловой) бифуркации

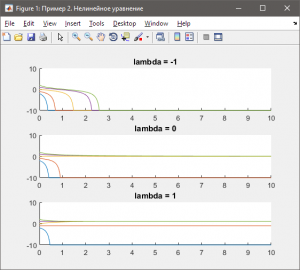
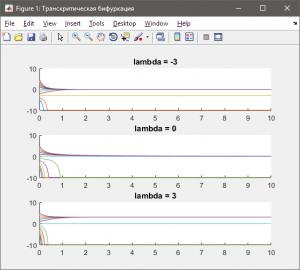
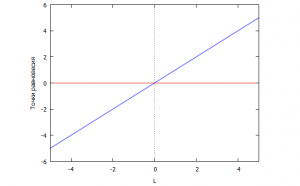
4.2 Транскритическая бифуркация (бифуркация типа «обмен устойчивости»)

Бифуркацию типа «обмен устойчивости» продемонстрируем на системе

\[\frac{{dx}}{{dt}} = x\lambda — {x^2}\]

Уравнение имеет два равновесных решения: \(x_1^{\rm{}} = 0,\;x_2^{\rm{}} = \lambda \). Первое решение устойчиво при и неустойчиво при ; второе – устойчиво при \(\lambda  < 0\) и неустойчиво при \(\lambda  > 0\). Принято говорить, что оба решения «обмениваются устойчивостью» в точке бифуркации \((x = 0,\;\lambda  = 0)\). На рис. 4.3, представлены соответствующие графики функций.

Рис. 4.3 — Временная характеристика системы с транскритической бифуркацией

Рис. 4.4 — Диаграмма транскритической бифуркации

4.3 Бифуркация «вилка»

Бифуркация типа «вилка» описывается ДУ вида

\[\frac{{dx}}{{dt}} = \lambda x — {x^3}\]

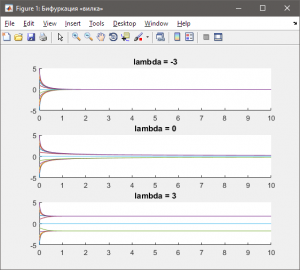
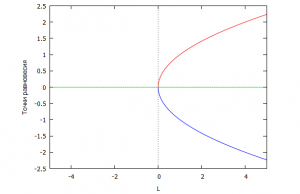
Это уравнение имеет одно равновесное решение \(x_1^{\rm{}} = 0 \) при  \(\lambda  < 0\) и три равновесных решения \(x_1^{\rm{}} = 0,\;x_{{\rm{2}}{\rm{,3}}}^{\rm{}} = \pm \sqrt \lambda \) при \(\lambda  > 0\). Соответствующие графики функций (рис. 4.6) симметричны относительно оси \(x\). В данном случае из точки бифуркации выходят три ветви равновесных состояний: две устойчивые и одна неустойчивая.

Рис. 4.5 — Временная характеристика системы с бифуркацией «Вилка»

Рис. 4.4 — Диаграмма бифуркации «Вилка»

Бифуркация типа «вилка» широко рассматривается в теоретической физике, поскольку на ней основываются некоторые теории, объясняющие спонтанное нарушение симметрии (устойчивая равновесная точка \(x_1^{\rm{}} = 0 \) при \(\lambda  < 0\) отвечает симметричному состоянию, например, отсутствию намагниченности, а рождающиеся устойчивые точки равновесия \({x^{\rm{}}} =  \pm \sqrt \lambda  \) при \(\lambda  > 0\) – состоянию с нарушенной симметрией). В частности, на этой бифуркации основана теория переходов II рода, предложенная Л. Д. Ландау. В ней чаще всего роль параметра \(\lambda\) играет отклонение температуры от критического значения, а величина \(x\) носит название «параметр порядка».
Рассмотренные бифуркации называются суперкритическими или нормальными. Их особенность заключается в том, что нелинейные члены \({x^2}\) и \({x^3}\) соответствующих уравнений оказывают влияние, способствующее получению устойчивых равновесных состояний системы. Однако при изменении знаков перед нелинейными членами, последние будут оказывать уже дестабилизирующее влияние на систему. В этих случаях возникают субкритические или обратные бифуркации.

4.4 Бифуркация Андронова – Хопфа (Hopf)

Кроме бифуркаций состояний равновесия в динамических системах при изменении параметра может происходить ещё одна перестройка структуры фазового портрета. Этот тип бифуркации рассматривает рождение предельного цикла из неподвижной точки и является более сложным, чем представленные выше.
Пусть нелинейная модель описывается следующим д. у.:

\[\frac{{dz}}{{dt}} = (\mu  + j\eta )z — z{\left| z \right|^2}\]

где  \(z \) – комплексная переменная; \(\mu + j\eta \) – комплексный параметр, причём \(j \) – мнимая единица,  \(\mu \) – варьируемый бифуркационный параметр.

Уравнение представляет собой комплексный аналог бифуркации типа «вилка». С целью определения всех равновесных решений необходимо произвести замену комплексной переменной \(z \):

\[z = {x_1} + j{x_2}\]

где \({x_1}\) и \({x_2}\) новые вещественные переменные.

В результате подстановки \(z \) в исходное ДУ получается система из двух уравнений первого порядка:

\[\begin{array}{l}
{{\dot x}_1} = [\mu — (x_1^2 + x_2^2)]{x_1} — \eta {x_2}\\
{{\dot x}_2} = [\mu — (x_1^2 + x_2^2)]{x_2} + \eta {x_1}
\end{array}\]

Таким образом, здесь осуществлён переход к модели второго порядка с вещественными параметрами. Полученные уравнения связаны между собой через комплексную переменную \(z \) и имеют следующие два стационарных решения:

\[{x_1} = {x_2} = 0 \  при \  z = 0 \\
x_1^2 + x_2^2 = {\left| z \right|^2} = \mu \ при \ z \ne 0\]

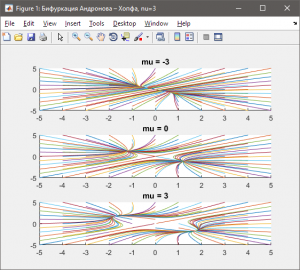
Первое решение является неустойчивым и совпадает с точкой бифуркации, а второе решение определяет окружность радиуса \(\sqrt \mu\) в пространстве координат \(({x_1},\;{x_2},\;\mu )\). На рис. 4.5 изображены фазовые траектории при фиксированных \(\mu \).

Рис. 4.5 — Фазовый портрет системы с бифуркацией Андронова – Хопфа

4.5 Бифуркации циклов

Образование в динамических системах второго порядка предельных циклов – соответствует бифуркации Андронова–Хопфа. Так, для модели, представленной системой ДУ

\[\begin{array}{l}
\frac{{d{x_1}}}{{dt}} = {x_2} — {x_1}(x_1^2 + x_2^2 — \lambda )\\
\frac{{d{x_2}}}{{dt}} = — {x_1} — {x_2}(x_1^2 + x_2^2 — \lambda )
\end{array}\]

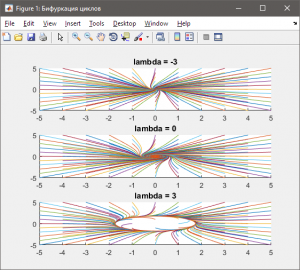
точка \(\lambda  = 0\) является бифуркационной точкой. При  изменении \(\lambda \) с отрицательных значений на положительные от нулевого равновесного состояния \(({x_1} = 0,{x_2} = 0)\) ответвляется периодическая орбита \(x_1^2 + x_2^2 = \lambda \), соответствующая устойчивому предельному циклу. При этом происходит изменение характера особой точки: из устойчивой она становится неустойчивой (рис. 4.6).

Рис. 4.6 — Фазовый портрет системы с бифуркацией циклов

4.6 Бифуркация удвоения периода

Теперь рассмотрим бифуркации отражений. Одномерное отображение – это простейшая модель эволюционного процесса, когда состояние системы характеризуется единственной переменной, а время – дискретно. Примером может служить динамика численности биологической популяции, если наблюдение за ее численностью производится, например, один раз в год.

Простейшей моделью, описывающей бифуркацию удвоения периода, может служить логистическое отображение

\[{x_{n + 1}} = 1 — \lambda x_n^2\]

Его неподвижные точки ищутся из решения соответствующего квадратного уравнения #\({x_0} = 1 — \lambda x_0^2\), так что

\[{x_0} = \frac{{ — 1 \pm \sqrt {1 + 4\lambda } }}{{2\lambda }}\]

При \(\lambda  = -0.25\) имеет место касательная бифуркация, в результате которой возникают неустойчивая и устойчивая точки.

Построим бифуркационную диаграмму (Рис. 4.7) с помощью команды математического пакета Maxima:

load(dynamics);
orbits(1-c*x^2,0,1,10,[c,-1,1],[style,dots],[nticks,1000]);

Рис. 4.7 — бифуркационная диаграмма системы (4.5)

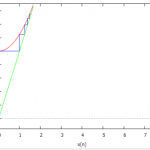
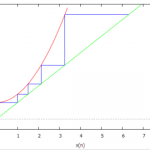
Также изменения поведения системы можно увидеть, построив итерационные диаграммы системы (Рис. 4.8):

staircase(1+0.1*x^2, 0, 5, [x, 0, 8]);
staircase(1+0.25*x^2, 0, 5, [x, 0, 8]);
staircase(1+0.5*x^2, 0, 5, [x, 0, 8]);

Рис. 4.8 — итерационные диаграммы системы

На построенных диаграммах видно, как устойчивая точка равновесия при \(\lambda  = -0.1\) теряет устойчивость при \(\lambda  = -0.25\) и неустойчива при \(\lambda  = -0.5\)

Источники

1. В. И. Арнольд, В. С. Афраймович, Ю. С. Ильяшенко, Л.П. Шильников, Теория бифуркаций. «Современны проблем математики. Фундаментальны направления. Т. 5 (Итог наук и техн. ВИНИТ А СССР)». М., 1985, 5—218
2. В. И. Арнольд, Теория катастроф «Современные проблемы математики. Фундаментальны направления. Т, 5(Итог наук и техн. ВИНИТ АН СССР)». М., 1985, 219—277
3. Теория бифуркаций динамических систем на плоскости / А.А.Андронов, Е.А.Леонтович, И.И.Гордон, А.Г.Майер .-М: Наука,1967.
4. Теория бифуркаций. Итоги науки и техники – фундаментальные направления. Т. 5. Современные проблемы математики. Динамические системы 5./ В.И.Арнольд, В.С.Афраймович, Ю.С. Ильяшенко, Л.П.Шильников. – М: ВИНИТИ, 1986, с. 5-218.
5. Шильников, Л.П. Гомоклинические траектории: от Пуанкаре до наших дней./ В книге: Математические события ХХ века. Изд.ФАЗИС, Москва, 2003, c.465-489.