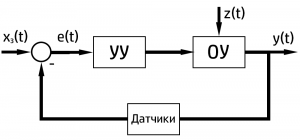
Для управления различными техническими объектами, часто используются ПИД-регуляторы. Для использования такого регулятора необходимо замкнуть объект управления обратной связью.
Рассмотрим пример реализации ПИД-регулятора в среде GX Works2 для контроллера Mitsubishi Electric Q02CPU
Рисунок 1 — Структурная схема объекта управления с обратной связью
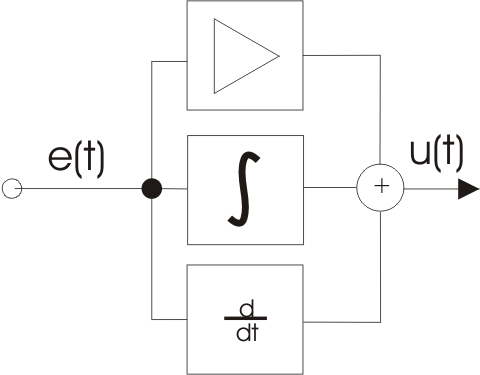
Структурную схему ПИД – регулятора изображенную на рисунке 2 представляют три параллельные ветви с пропорциональным, интегральным и дифференциальным звеном, выход каждого из которых при-ходит на сумматор, в результате чего получаем управляющее воздействие.
Рисунок 2 — Структурная схема ПИД – регулятора
Реализацию необходимо осуществить, начиная с построения про-порционального управления, в этом случае воздействие будет изменяться пропорционально ошибке. Реализация П – закона в среде Mitsubishi GX Works2 представлена на рисунке 3
Рисунок 3 — Получение пропорциональной составляющей ПИД-закона
Для получения пропорциональной составляющей управления P_ControlAction необходимо получить ошибку Error и затем умножить ее на коэффициент пропорциональности Kp. Вычисление ошибки произво-дится путем вычитания из заданного значения угла SetValue величины те-кущего положения маятника AngleBin.
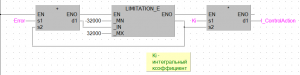
Вторым этапом реализации регулятора является вычисление интегральной составляющей управления. Интегратор необходим для устранения статической ошибки. Величина управляющего воздействия пропорциональна интегралу по времени от ошибки. Для полноты понимания, представим реализацию интегральной части ПИД – контроллера на рисунке 4.
Рисунок 4 — Получение интегральной составляющей воздействия
В среде GX Works2 интегратор реализуется блоком сложения, далее блок LIMITATION_E позволяет предотвратить переполнение переменной с накопленной ошибкой, по мере накопления ошибки результат сложения умножается на интегральный коэффициент Ki, и произведение записывает-ся в переменную I_ControlAction.
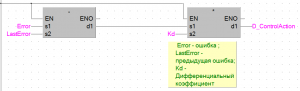
Для улучшения качества процесса необходима реализация Д – воздействия, для этого необходимо знать не только ошибку, но и скорость ее изменения, это можно реализовать вычислением ошибки в момент времени t и в момент времени t+1, на рисунке 5 покажем как выглядит описанный алгоритм.
Рисунок 5 — Получение дифференциальной составляющей управления
Чтобы получить дифференциальную составляющую D_ControlAction, необходимо умножить разницу ошибок в моменты времени t и t-1 на дифференциальный коэффициент Kd.
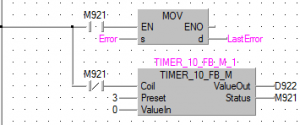
На рисунке 6 показан алгоритм сохранения в памяти ошибки в момент времени t-1
Рисунок 6 — Запись в память ошибку в момент времени t-1
В алгоритме, показанном на рисунке 6, используется таймер с периодом в 10 мс, каждые 3 периода включается блок MOV и в переменную LastError записывается текущее значение ошибки.
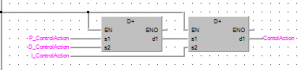
Для получения управляющего воздействия необходимо сложить все три составляющие управления, после чего результат записывается в переменную ControlAction.
Последний элемент реализации ПИД–контроллера на языке релейных диаграмм, представлен на рисунке 7.
Рисунок 7 — Получение управляющего воздействия