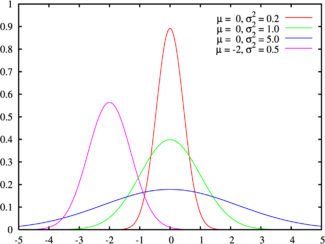
В заметке рассмотрены основные свойства математического ожидания и дисперсии с доказательствами.
В статье приняты следующие обозначения:
\(a \) — неслучайная величина (константа)
\(X, Y \) — случайные величины
\(M[X]\) — Математическое ожидание X
\(D[X]\) — Дисперсия X
Математическое ожидание
Математическое ожидание неслучайной величины
\[ M[a] = a\]
Доказательство:
Доказать, это достаточно очевидное, свойство можно, рассматривая неслучайную величину как частный вид случайной, при одном возможном значении с вероятностью единица; тогда по общей формуле для математического ожидания:
\[ M[a] = a * 1 = a \]
Математическое ожидание линейно
\[ M[aX + bY] = aM[X] + bM[Y]\]
Доказательство вынесения неслучайной величины за знак математического ожидания
\[ M[aX] = a M[X] \]
Доказательство прямо следует из линейности суммы и интеграла.
Следует специально отметить, что теорема сложения математических ожиданий справедлива для любых случайных величин — как зависимых, так и независимых.
Теорема сложения математических ожиданий обобщается на произвольное число слагаемых.
Для дискретных величин
\[ M[aX] = \sum_{i} a x_i p _i = a \sum_{i} x_i p_i = a M[X]\]
Для непрерывных величин
\[ M[aX] = \intop_{ \infty }^{\infty} a x f(x) dx = a \intop_{ \infty }^{\infty} x f(x) dx = a M[X]\]
Доказательство математического ожидания суммы случайных величин
а) Пусть \((X, Y) \) — система дискретных случайных величин. Применим к сумме случайных величин общую формулу для математического ожидания функции двух аргументов:
\[ M[X + Y] = \sum_{i} \sum_{j} (x_i + y_i) p_{ij} \\
= \sum_{i}\sum_{j} x_i p_{ij} + \sum_{i}\sum_{j} y_i p_{ij} \\
= \sum_{i} x_i\sum_{j} p_{ij} + \sum_{j} y_j\sum_{i} p_{ij} \]
Но \(\sum_{j} p_{ij} \) представляет собой не что иное, как полную вероятность того, что величина \(X \) примет значение \(x_i \):
\[ \sum_{j} p_{ij} = P(X = x_i) = p_i \]
следовательно,
\[ \sum_{i} x_i\sum_{j} p_{ij} = \sum_{i} x_i p_i = M[X] \]
Аналогично докажем, что
\[ \sum_{j} y_j\sum_{i} p_{ij} = M[Y] \]
б) Пусть \((X, Y) \) — система непрерывных случайных величин.
\[ M[X + Y] = \int \intop_{ \infty }^{\infty } (x+y) f(x,y) dx dy = \int \intop_{ \infty }^{\infty } x f(x,y) dx dy + \int \intop_{ \infty }^{\infty } y f(x,y) dx dy \]
Преобразуем первый из интегралов:
\[ \int \intop_{ \infty }^{\infty } x f(x,y) dx dy = \intop_{ \infty }^{\infty } x (\intop_{ \infty }^{\infty } f(x,y)dy) dx = \intop_{ \infty }^{\infty } x f_1(x) dx = M[X] \]
аналогично второй:
\[ \int \intop_{ \infty }^{\infty } y f(x,y) dx dy = M[X] \]
Математическое ожидание произведения
Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
\[ M[XY] = M[X] M[Y] + cov(XY)\]
для независимых величин:
\[ M[XY] = M[X] M[Y] \]
Доказательство
Будем исходить из определения корреляционного момента:
\[ cov(X,Y) = M[ \stackrel{ \circ }{X} \stackrel{ \circ }{Y} ] = M[(X- M[X])(Y-M[Y])] \]
Преобразуем это выражение, пользуясь свойствами математического ожидания:
\[ cov(X,Y) = M[(X- M[X])(Y-M[Y])] = \\
M[XY] — M[X] M[Y] — M[Y]M[X] + M[X]M[Y] = \\
M[X Y] — M[X] M[Y] \]
что, очевидно, равносильно доказываемому соотношению
Дисперсия
Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около её математического ожидания.
\[ D[X] = M[X^2] — (M[X])^2 \]
Дисперсия не зависит от знака
\[ D[-X] = D[X] \]
Дисперсия суммы случайной и постоянной величин
\[ D[X+b] = D[X] \]
Дисперсия неслучайной величины
\[ D[a] = 0 \]
Доказательство:
По определению дисперсии:
\[ D[a] = M[\stackrel{ \circ }{a^2}] = M[a — M[a]^2 ] = M[(a-a)^2] = M[0] = 0\]
Дисперсия суммы случайных величин
\[ D[X+Y] = D[X] + D[Y] + 2*cov(X,Y) \]
Доказательство:
Обозначим \(XY = Z \).
По теореме сложения математических ожиданий:
\[ M[Z] = M[X] + M[Y] \]
Перейдем от случайных величин \(X, Y, Z \). к соответствующим центрированным величинам \(\stackrel{ \circ }{X}, \stackrel{ \circ }{Y}, \stackrel{ \circ }{Z} \), имеем:
\[ \stackrel{ \circ }{Z} = \stackrel{ \circ }{X} + \stackrel{ \circ }{Y} \]
По определению дисперсии
\[ D[X+Y] = D[Z] = M[\stackrel{ \circ }{Z}^2] = M[\stackrel{ \circ }{X}^2] + 2M[\stackrel{ \circ }{X} \stackrel{ \circ }{Y}] + M[\stackrel{ \circ }{Y}^2] \\
= D[X] + 2 cov(X,Y) + D[Y] \]
Дисперсия произведения неслучайной величины на случайную
\[ D[aX] = a^2 D[X]\]
Доказательство:
По определению дисперсии
\[ D[aX] = M[(a X — M[a X])^2] = M[(a X — a M[X])^2] = a^2 M[(X — M[X])^2] = c^2 D[X] \]
Дисперсия произведения независимых величин
\[ D[XY] = D[X] D[Y] + (M[X])^2 D[Y] + (M[Y])^2 D[X]\]
Доказательство:
Обозначим \(XY = Z \). По определению дисперсии
\[ D[XY] = D[Z] = M[Z^2] = M[Z-M[Z]]^2\]
Так как величины \(XY\) независимы, то \(M[Z] = M[X]M[Y]\) и
\[ D[XY] = M[(XY — M[X]M[Y])^2] \\
= M[X^2 Y^2] — 2M[X]M[Y]M[XY]+ M[X]^2M[Y]^2 \]
При независимых \(XY\) величины \(X^2Y^2\) также независимы, следовательно:
\[ M[X^2 Y^2] = M[X^2] M[Y^2], M[XY] = M[X]M[Y]\]
и
\[ D[XY] = M[X^2]M[Y^2] — M[X]^2M[Y]^2 \]
но \(M[X]^2\) есть не что иное, как второй начальный момент величины \(X\) , и, следовательно, выражается через дисперсию:
\[ M[X^2] = D[X]+M[X]^2 \]
аналогично
\[ M[Y^2] = D[Y]+M[Y]^2 \]
Подставляя эти выражения и приводя подобные члены, приходим к формуле
\[ D[XY] = D[X] D[Y] + (M[X])^2 D[Y] + (M[Y])^2 D[X]\]