В работе поднимается проблема анализа надёжности сложных систем управления, применяемых в ответственных областях науки и техники, например, таких как объекты использования атомной энергии. Приводится обзор основных принципов оценки показателей надёжности на примере вероятности безотказной работы. Обосновывается требование к автоматизированному расчёту, необходимость разработки программного-алгоритмического комплекса для расчета показателей надежности, и основной перечень требований к нему. Делается обзор текущего состояния разработки программно-алгоритмического комплекса и перспективы развития.

I. ВВЕДЕНИЕ

При проектировании современных систем для объектов использования атомной энергии немаловажным этапом проектирования является проектная оценка надёжности системы [1]. Для достижения требуемых показателей надежности используются различные стратегии, такие как резервирование, мажорирование, организация отказоустойчивых систем и использования комплектов запасного имущества и принадлежностей (ЗИП). В последнем случае восстановление функционирования сводится к замене отказавшего модуля работоспособной запасной частью, что может быть выполнено эксплуатационными персоналом. Комплект ЗИП-О является достаточно эффективным методом повышения надёжности резервированных систем, однако, из-за ограничений на суммарную стоимость и количество начальных запасов в комплекте ЗИП необходимо находить компромисс между показателями надёжности и стоимостью систем.

Влияние комплекта ЗИП на показатели надёжности системы существенно зависит от соотношения между временем замены отказавшего элемента работоспособной запасной частью и допустимым временем перерыва в работе системы. Здесь возможны три варианта:

• если из-за инерционности или дискретности протекающих в системе процессов перерыв на замену вышедших из строя частей (может быть несколько десятков минут) не приводит к нарушению качества ее функционирования, то в модели надёжности время замены можно не учитывать;
• если резерв времени, создаваемый инерционностью процессов, сравним с временем замены, то при оценке надежности надо использовать модели надежности с мгновенно пополняемым резервом времени [1];
• третий вариант: допустимое время перерывов в работе мало настолько, что за это время невозможно выполнить замену отказавшего модуля. В таком случае, комплект ЗИП не может обеспечить повышение показателей надежности, т. е. эффективность его создания близка к нулю. Тогда для обеспечения эффективности применения ЗИП необходимо использование встроенного структурного резервирования

Работоспособность системы на время замены обеспечивается структурным резервом. [2]

Заметим, что использование структурного резервирования во втором и третьем случаях сводит задачу к первому случаю с достаточным временем на замену.

Так как современные системы могут насчитывать десятки и сотни компонентов, которые необходимо учитывать при анализе надёжности, а формулы вычисления надёжности компонента с ЗИП и учёта влияния структуры на итоговую надежность системы достаточно сложны, то ручное аналитическое вычисление практически не реализуемо, что приводит к необходимости использования автоматических средств расчёта показателей надежности по надёжностным схемам систем и дальней параметрической оптимизации системы (в качестве параметра рассматривается комплект ЗИП-О).

В мире существует всего несколько программных продуктов, способных произвести расчёт, но все из них реализуют только один из способов оценки надёжности: аналитический или моделирование. При этом из-за значительных погрешностей аналитического метода и экспериментального характера второго необходима верификация полученных результатов, что проще всего сделать с помощью сравнения результатов, полученных обоими способами, однако для этого было бы необходимо приобретать несколько комплектов программного обеспечения и реализовывать модель для каждой из систем.

Исходя из вышесказанного было решено разработать программно-алгоритмический комплекс, реализующий расчёт показателей надежности аналитическим и экспериментальным способом.

II. МЕТОДЫ ОЦЕНКИ НАДЁЖНОСТИ

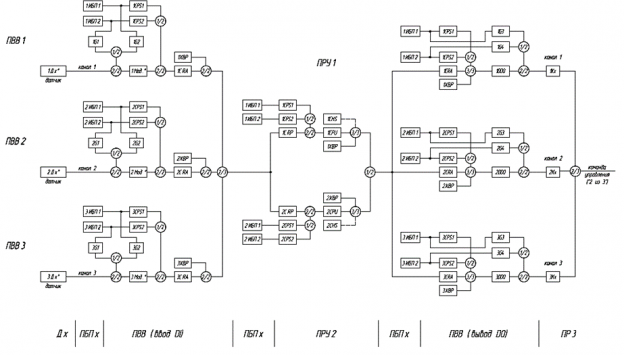
Исходными данными для оценки надёжности системы являются: структурно-надёжностная схема (Рисунок 1), перечень компонентов с указанием показателей надежности (как правило, интенсивность отказов или среднее время безотказной работы) и стоимости, целевые показатели надежности для рассматриваемых систем.

Существует два глобальных типа методов: теоретические и экспериментальные. Теоретические методы основаны на непосредственном вычислении интересующих значений через известные или выводимые математические выражения из известных параметров системы. Экспериментальные методы делятся на натурные, полунатурные и синтетические, очевидно, что в случае с проектируемой сложной и дорогостоящей системой натурные и полунатурные эксперименты невозможны, особенно с учётом того, что требуемые характеристики имеют вероятностный характер. Экспериментальный метод для оценки случайных параметров — имитационное моделирование, в частности предлагается использовать дискретно-событийное моделирование в силу особенностей исходных данных.

A. Аналитическая оценка надежности

Для лучшего масштабирования процессов моделирования предлагается разделить систему на несколько уровней иерархии:

• Компонентный уровень. На этом уровне располагаются элементарные компоненты системы, для которых существует понятие комплекта ЗИП (например, контроллеры, модули ввода-вывода и другие).
• Операционный уровень. Этот уровень, на котором, как правило, задаются требования по показателям надёжности, описывает структуру влияния работоспособности компонентов на выполнение функциональной операции в системе.
• Системный уровень. На этом уровне описывается структура влияния успешности выполнения операции на отказы уровня системы и оцениваются итоговые показатели надёжности системы.

При такой декомпозиции понятие ЗИП-О становится справедливым только для отдельных компонентов и не требуется использование сложных выражений для учёта ЗИП-О для структуры, а только для учёта показателей надёжности отдельных компонентов. Таким образом, второй уровень оперирует с компонентами, имеющими конечное рассчитанное значение показателей надежности, что даёт право использовать формулы теории вероятностей для расчета показателей надёжности различных типов связи компонентов между собой, таких как последовательное (нерезервированное), резервированное и мажорированное (в различных сочетаниях) соединения. Второй и третий уровень отличаются тем, что на втором уровне производится оптимизация комплектов ЗИП-О, а третий уровень оперирует подсистемами, которые могут иметь несколько входов и выходов, в том числе, с различными показателями надежности, но оптимизация не производится в силу чрезмерного числа параметров.

На рисунке 2 показан иерархический подход (стрелками обозначены отношения расчёта показателей надежности), где на нулевом уровне находятся элементарные компоненты, с возможностью формирования ЗИП-О, причём элементы любой глубины вложения могут состоять между собой в отношениях, описанных ранее (нерезервированное соединение, резервирование и т.д.).

Расчёт такой модели ведётся с использованием однотипных операций, что позволяет легко масштабировать модель.

После построения расчётной модели, где комплекты ЗИП-О являются переменными, производится оптимизация комплекта с целью получения требуемых показателей надежности при минимальной стоимости.

В качестве примера аналитического расчета показателей надёжности компонента с учетом ЗИП-О, приведем расчет такого показателя надежности, как вероятность безотказной работы при периодическом пополнении запасов (что соответствует российской структуре планового финансирования, когда закупки планируются на последующие периоды без возможности экстренных закупок).

Так как в рассматриваемых системах отсутствуют структурно-нерезервированные компоненты, то можно принять, что время на замену отказавшего элемента на запасной много меньше максимально допустимого. Тогда вероятность отказа рассматриваемого компонента приблизительно равна вероятности достаточности ЗИП.

Вероятность достаточности ЗИП \({P_Д}(t)\) есть вероятность того, что любая заявка на ЗЧ в комплект ЗИП в заданном интервале времени (периоде пополнения, интервале функционирования) будет удовлетворена за счёт запасов в комплекте ЗИП-О.

При периодическом пополнении запасов и потоке заявок kλ и L запасных частях вероятность достаточности ЗИП и вероятность безотказной работы:

\[{P_c}(t,L) = 1 — I(A,L + 1),A = k\lambda T\]

где \(I( x,m )\) — функция распределения Эрланга, неполная гамма-функция:

\[I(x,m) = 1 — \sum\limits_{i = 0}^{m — 1} {\frac{{{x^i}}}{{i!}}} {e^{ — x}}\]

B. Оценка надёжности методом имитационного моделирования

Альтернативным и дополнительным в нашем случае методом оценки надёжности является метод, основанный на имитационном моделировании. В случае анализа показателей надёжности с учетом особенности представления исходных данных по надёжности компонентов в формате интенсивности отказов в час больше всего подходит принцип дискретно-событийного моделирования, где одно событие эквивалентно часу работы системы.

В рассматриваемом методе предполагается, что каждый компонент системы является источником неисправности.

Для реализации метода подходит подготовленная для аналитического метода структура модели, однако необходимо дополнить элементарные компоненты генераторами случайных чисел, имитирующими возникновение отказа в компоненте и счётчик комплектов ЗИП-О для анализа его использования.

Для вычисления показателей надёжности производится многократное моделирование работы в течение определенных периодов времени с учётом заданного комплекта ЗИП-О.

Заметим, что прямая оптимизация комплекта ЗИП при использовании в качестве критерия отказа системы «отсутствие сигнала на выходах» и значительного структурного резервирования, практически не реализуема в силу чрезмерно большого числа требуемых вычислений.

III. РЕАЛИЗАЦИЯ СИСТЕМЫ

На начальном этапе развития принято решение создания расчётного ядра на языке Python [3], [4], [5] для возможности простого интегрирования в графические интерфейсы пользователей в будущем.

Так как предполагаемый алгоритм расчёта сводится к формированию и вычислению графа и последующей его оптимизации, причём число оптимизируемых переменных может быть очень велико для традиционных методов оптимизации, то было принято решение использовать библиотеку TensorFlow [3], являющуюся достаточно низкоуровневой для реализации графа, но при этом имеющую в себе компоненты для расчёта и реализации специальных математических функций, необходимых для вычисления показателей надёжности и включающую в себя мощные инструменты оптимизации, разработанные для нейронных сетей, где число оптимизируемых величин может быть очень велико.

Библиотека выбрана исходя из требований к распространённости и активности поддержки. TensorFlow разрабатывается при поддержке Google Inc. и применяется в значительной части современных исследований, связанных с вычислениями больших графов (в частности нейронных сетей), в связи с этим в библиотеке реализовано большое количество алгоритмов оптимизации параметров графа и других статистических инструментов.

В силу особенностей используемой расчётной библиотеки для создания расчетной модели необходимо ручное написание исходного кода модели или реализация его автоматической генерации из формального описания, полученного из графического интерфейса. На уровне модели описывается только структура и исходные параметры, а методика расчёта реализована в ядре расчётной библиотеки, что позволяет корректировать методику и дополнять перечень оцениваемых параметров без изменения моделей, таким образом реализуется полная обратная совместимость с программными моделями для предыдущих версий.

На данном этапе развития программно-алгоритмического комплекса в рассматриваемых системах встречаются три типа использования компонентов, имеющих ЗИП-О: без резервирования, с резервированием (дублированием) и мажорированием, но так как перечень схем резервирования не ограничивается ими, реализован универсальный интерфейс создания типов соединений, позволяющий легко расширять перечень рассчитываемых критериев надёжности и добавлять новые типы резервирования.

Особого внимания заслуживает процедура оптимизации комплекта ЗИП-О при аналитическом расчёте. Так как теоретическая расчётная модель является дискретной, а дискретная оптимизация, строго говоря, является не решенной проблемой, что в сочетании с большой размерностью оптимизируемых моделей (от 50 до 100 параметров на каждую модель) приводит к сложности непосредственной оптимизации.

Для решения описанной проблемы ступенчатая функция изменения показателей надёжности от размера комплекта ЗИП-О аппроксимирована непрерывной функцией с незначительным значением производной в дробных значениях комплекта ЗИП, что позволяет использовать непрерывную оптимизацию, но при этом учитывает скачкообразное повышение стоимости комплекта ЗИП и показателей надёжности при переходе через целое значение комплекта. Такой подход позволяет использовать методы стохастического градиентного спуска и достаточно эффективно оптимизировать комплект.

IV. ЗАКЛЮЧЕНИЕ

На данный момент создан рабочий прототип расчётной библиотеки для аналитического вычисления показателей надежности, в ближайшее время планируется реализация визуализации расчетной модели на Tensor Board и реализация метода оценки показателей надежности на базе моделирования. Полученные результаты используются в ряде работ, по теме проектной оценки надёжности сложных систем управления для объектов использования атомной энергии.

Полученные результаты позволяют достаточно быстро в ручном режиме создавать программные модели оцениваемых систем, проводить в автоматическом режиме оптимизацию комплекта ЗИП-О и создавать отчеты с результатами расчётов для использования в проектной документации.

В ближайшей перспективе — реализация дискретно-событийного моделирования для верификации полученных результатов аналитического расчёта и оптимизации, а также реализация визуализации расчетной модели на базе TensorBoard.

В дальнейшем планируется создание графического интерфейса пользователя, а также универсального интерфейса работы вычислительного ядра и интерфейса, в том числе с возможностью размещения вычислительного модуля и графического интерфейса на разных ЭВМ, что позволит работать с системой людям не знакомым с необходимыми языками программирования и предоставлять безопасный (в смысле защиты программного продукта) доступ для расчёта заинтересованным лицам.

СПИСОК ЛИТЕРАТУРЫ

1. IEC 61226:2009 Nuclear power plants – Instrumentation and control important for safety – Classification of instrumentation and control functions, International Electrotechnical Commission, 2009 for safety – Classification of instrumentation and control
2. IEC 60050: International Electrotechnical Vocabulary
3. Алексеев О. Г., Володось И. Ф. Оптимизация состава комплекта запасных элементов для технических средств АСУ// Надежность и контроль качества, 1978, № 12.
4. Черкесов Г. Н. Оценка надежности систем с учетом ЗИП: учеб. пособие. — СПб.: БХВ-Петербург, 2012. — 480 с.
5. Travis E. Oliphant. Python for Scientific Computing // Computing in Science & Engineering. 2007, вып. 9. С. 10-20.
6. Jarrod Millman and Michael Aivazis. Python for Scientists and Engineers // Computing in Science & Engineering. 2011, вып. 13. С. 9-12.
7. Stéfan van der Walt, S. Chris Colbert and Gaël Varoquaux. The NumPy Array: A Structure for Efficient Numerical Computation // Computing in Science & Engineering. 2011, вып. 13. С. 22-30.
8. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. J. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mane, R. Monga, S. Moore, D. G. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. A. Tucker, V. Vanhoucke, V. Vasudevan, F. B. Viegas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu, and X. Zheng. TensorFlow: Large-scale machine learning on heterogeneous distributed systems. // Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI ’16), Savannah, GA, USA, November 2–4, 2016

Библиографические данные статьи

М. Ю. Шестопалов, Д. И. Каплун, А. М. Синица, К. М. Жеронкин, М. А. Ельшин. Разработка программно-алгоритмического комплекса для оценки надежности и оптимизации систем с ЗИП // Сб. докладов XVI Международная конференция по мягким вычислениям и измерениям SCM-2018, Изд-во СПбГЭТУ «ЛЭТИ», 23-25 мая, т.1, 2018, С. 570-573