Что такое флуктуационный анализ и зачем он нужен?
Представьте, что вы наблюдаете за уровнем воды в реке. Иногда вода спокойна, иногда бушует. Эти изменения — флуктуации. Мы видим подобные явления повсюду: цены на акции, пульс сердца, трафик сайта, даже ваше настроение в течение дня.
Но что, если среди этого хаоса есть скрытый порядок? Что, если сегодняшние изменения как-то связаны с тем, что произойдет завтра? Именно это помогает выяснить флуктуационный анализ.
В рамках заметки рассмотрим продвинутую версию флуктуационого анализа — Detrended Fluctuation Analysis (DFA). Этот метод помогает обнаружить долгосрочные корреляции в данных, даже когда они маскируются под шум или имеют нестационарные тренды.
Почему обычные методы не работают?
Простые статистические методы часто ломаются, когда данные:
- Имеют меняющиеся тренды (например, растущие или падающие участки)
- Содержат шум разной интенсивности
- Не являются стационарными (их статистические свойства меняются во времени)
DFA специально создан для работы с такими сложными данными. Он «очищает» временной ряд от локальных трендов и оценивает, насколько сильно флуктуации коррелируют на разных временных масштабах.
Показатель Херста: магическое число долгосрочной памяти
Ключевой результат DFA — показатель Херста (Hurst exponent). Это число больше 0 до 1, которое расскажет вам о характере ваших данных:
- H = 0.5: Данные ведут себя как обычное броуновское движение. Прошлое не влияет на будущее — каждое изменение случайно и независимо от предыдущих. Пример: идеальный случайный блуждающий процесс.
- H > 0.5: Данные имеют персистентное поведение. Если значения росли, они скорее всего продолжат расти. Система «помнит» свои предыдущие состояния. Пример: трендовые финансовые рынки или климатические изменения.
- H < 0.5: Данные антиперсистентны. Система стремится к возврату к среднему значению. Если значения росли, скорее всего, последует падение. Пример: волатильные рынки или многие биологические процессы.
Как работает Detrended Fluctuation Analysis (DFA)?
DFA — это относительно простой и эффективный метод, который помогает найти показатель Херста. Он работает по простому принципу:
- Разбиваем данные на окна разного размера.
- В каждом окне убираем локальные тренды (отсюда «detrended»).
- Считаем, насколько данные флуктуируют вокруг этих трендов.
- Строим график зависимости флуктуаций от размера окна.
- Наклон этого графика в логарифмических осях и есть показатель Херста.
Практика: DFA с библиотекой FluctuationAnalysisTools
Теперь перейдем к практической части. Для работы с DFA в Python существует отличная библиотека FluctuationAnalysisTools, доступная на PyPI. Рассмотрим, как с ней работать.
Установка библиотеки
Сначала установим необходимый пакет:
pip install "FluctuationAnalysisTools<2.0.0"Базовые концепции библиотеки
В рамках заметки мы будем использовать два основных инструмента из библиотеки:
generate_fbn()— генерирует дробное броуновское движение с заданным показателем Херста для тестированияdfa()— выполняет DFA анализ на ваших данных
Шаг 1: Генерация тестовых данных с известным показателем Херста
Сначала научимся создавать данные, где мы точно знаем значение H. Это поможет нам понять, как работает метод.
import numpy as np
from StatTools.generators import generate_fbn
# Параметры для генерации
hurst = 0.75 # Задаем показатель Херста (0.75 означает сильную трендовую память)
length = 1000 # Длина временного ряда
# Генерируем fractional Brownian noise с помощью метода Kasdin
fbn_series = generate_fbn(hurst=hurst, length=length, method="kasdin")
print(f"Сгенерирован временной ряд с H = {hurst}")
print(f"Длина ряда: {len(fbn_series)} точек")
print(f"Первые 10 значений: {fbn_series[0, :10]}")Этот код создаст временной ряд, в котором каждое следующее значение зависит от предыдущих с заданной «силой памяти» (hurst=0.75).
Шаг 2: Применение DFA для оценки показателя Херста
Теперь самое интересное — анализируем наши данные с помощью DFA:
from StatTools.analysis.dfa import dfa
from scipy import stats
import numpy as np
# Применяем DFA анализ
s_vals, f2_vals = dfa(fbn_series, degree=2, processes=2)
print("Результаты DFA анализа:")
print(f"- Количество размеров окон: {len(s_vals)}")
print(f"- Первые 5 размеров окон: {s_vals[:5]}")
print(f"- Первые 5 значений F^2: {f2_vals[:5]}")
# Оцениваем показатель Херста из лог-лог зависимости
log_s = np.log(s_vals)
log_f = np.log(np.sqrt(f2_vals)) # Берем корень из F^2, чтобы получить F
res = stats.linregress(log_s, log_f)
estimated_h = res.slope
print(f"\nРеальный показатель Херста: {hurst}")
print(f"Оцененный показатель Херста: {estimated_h:.4f}")
print(f"Относительная погрешность: {abs(estimated_h - hurst)/hurst:.2%}")Шаг 3: Продвинутая визуализация результатов DFA
Библиотека FluctuationAnalysisTools предлагает мощные инструменты для визуализации. Давайте используем их для более глубокого понимания результатов:
from StatTools.analysis.utils import analyse_zero_cross_ff
from StatTools.visualization.plot_ff import plot_ff
import matplotlib.pyplot as plt
# Анализ функции распределения нулевых пересечений
fig, axs = plt.subplots(figsize=(10, 6))
# Calculate Hurst exponent from fluctuation function
f_vals = np.sqrt(f2_vals).reshape(1, -1) # Convert F^2(s) to F(s) and reshape for analysis
s_vals_2d = s_vals.reshape(1, -1) # Reshape scales to 2D array
ff_parameters, residuals = analyse_zero_cross_ff(f_vals, s_vals_2d)
# Построение графика
plot_ff(
f_vals,
s_vals,
ff_parameter=ff_parameters,
residuals=residuals,
ax=axs
)
# Настройка графика
plt.title('Анализ флуктуационной функции\n'
f'Реальный H = {hurst}, Оцененный H = {estimated_h:.4f}',
fontsize=14, fontweight='bold')
plt.xlabel('Размер окна (s)', fontsize=12)
plt.ylabel('Значение функции распределения', fontsize=12)
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()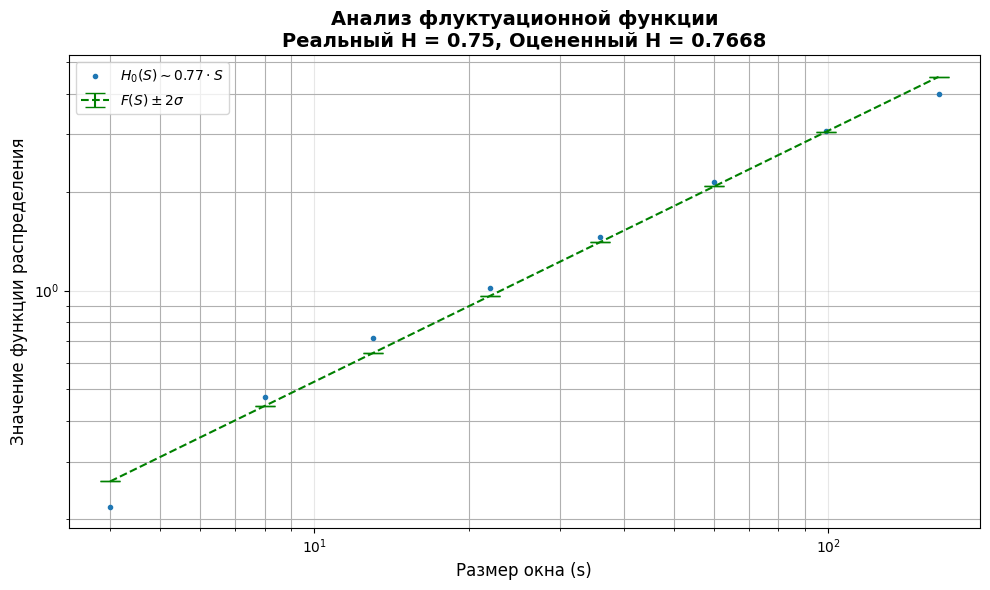
Шаг 4: Анализ нескольких временных рядов одновременно
Одна из сильных сторон библиотеки — возможность обрабатывать множество рядов параллельно. Это особенно полезно для больших наборов данных:
# Генерируем несколько временных рядов с разными показателями Херста
hurst_values = [0.3, 0.5, 0.7, 0.9]
all_series = []
for h in hurst_values:
series = generate_fbn(hurst=h, length=2000, method="kasdin")
all_series.append(series[0])
# Преобразуем в numpy массив для пакетной обработки
data_array = np.array(all_series)
# Применяем DFA ко всем рядам одновременно (параллельная обработка)
s_vals_multi, f2_vals_multi = dfa(data_array, degree=2, processes=4)
print("\nАнализ нескольких временных рядов:")
print(f"Форма результатов F²: {f2_vals_multi.shape}")
print("Оцененные показатели Херста:")
# Оцениваем H для каждого ряда
estimated_h_values = []
for i, h_target in enumerate(hurst_values):
log_f = np.log(np.sqrt(f2_vals_multi[i]))
slope = stats.linregress(np.log(s_vals_multi), log_f).slope
estimated_h_values.append(slope)
accuracy = abs(slope - h_target) / h_target * 100
print(f" Ряд {i+1}: H_реальный = {h_target:.2f}, H_оцененный = {slope:.4f}, точность = {100-accuracy:.1f}%")Практические советы для начинающих
- Длина данных важна: Для точной оценки H нужны временные ряды длиной минимум 500-1000 точек. Чем длиннее ряд, тем надежнее результат.
- Выбор степени полинома: Параметр
degreeв функцииdfaопределяет, какая степень полинома используется для удаления трендов. Обычно:degree=1— линейные трендыdegree=2— квадратичные тренды (наиболее распространенный выбор)degree=3— кубические тренды
- Параллельная обработка: Для больших наборов данных используйте параметр
processesдля ускорения вычислений. На современных компьютерах можно использовать 4-8 процессов. - Валидация результатов: Всегда проверяйте результаты на синтетических данных с известным H перед анализом реальных данных. Это поможет понять точность метода для ваших конкретных условий.
- Интерпретация в контексте: Показатель Херста сам по себе не дает полной картины. Комбинируйте его с другими методами анализа временных рядов и всегда учитывайте предметную область.
Что почитать?
- Kasdin, N. J. (1995) — Discrete simulation of colored noise and stochastic processes and 1/fα power law noise generation. DOI:10.1109/5.381848.
Исходный источник метода, реализованного вgenerate_fbn - Mandelbrot & Van Ness (1968) — Fractional Brownian Motions, Fractional Noises and Applications
Теоретический фундамент: оригинальное определение fBm через стохастический интеграл. - Bogachev M. at al. (2023) Understanding the complex interplay of persistent and antipersistent regimes in animal movement trajectories…
Пример практического применения DFA в биомедицинских исследованиях: количественная оценка поведенческих изменений при тестировании анксиолитиков через анализ H в траекториях движения. Показывает, как фрактальный анализ помогает выявлять тонкие эффекты, ускользающие от традиционных метрик.
Блокнот на Kaggle: https://www.kaggle.com/code/user164919/dfa-python
