Это вводная статья, призванная познакомить людей, не знакомых с компьютерным зрением, с проблемой классификации изображений и data-driven подходом.

Классификация изображений

В этом разделе рассмотрена задача классификации изображений, которая представляет собой задачу присвоения входному изображению одной метки из фиксированного набора. Это одна из базовых проблем компьютерного зрения, которая, несмотря на свою простоту, имеет большое разнообразие практических применений. Более того, как мы увидим позже, многие другие, казалось бы, различные задачи компьютерного зрения (такие как обнаружение объектов, сегментация) могут быть сведены к классификации изображений.

Пример

Например, на рисунке ниже модель классификации изображений берет один образ и присваивает вероятности 4 меткам, {cat, dog, hat, mug}. Имейте в виду, что для компьютера изображение представляется в виде одного большого трехмерного массива чисел. В этом примере изображение кошки имеет ширину 248 пикселей, высоту 400 пикселей и имеет три цветных канала красный, зеленый, синий (или RGB для краткости). Таким образом, изображение состоит из 248x400x3 чисел, или в общей сложности 297 600 чисел. Каждое число — это целое число в диапазоне от 0 (черное) до 255 (белое). Наша задача — превратить эту четверть миллиона цифр в единую метку, например “cat”.

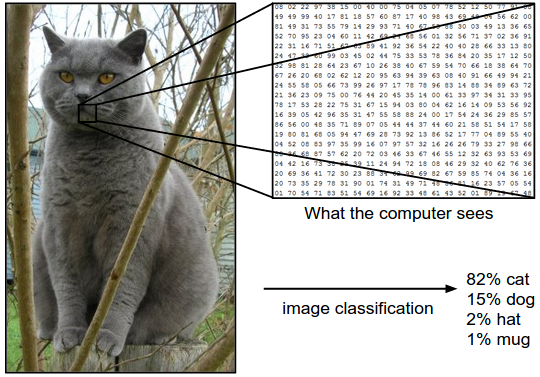
Проблемы

Поскольку задача распознавания визуального концепта (например, кошки) является относительно тривиальной для человека, стоит рассмотреть связанные с ней проблемы с точки зрения алгоритмов компьютерного зрения. Поскольку ниже представлен (неисчерпаемый) список проблем, помните о первичном представлении изображений в виде трехмерного массива:

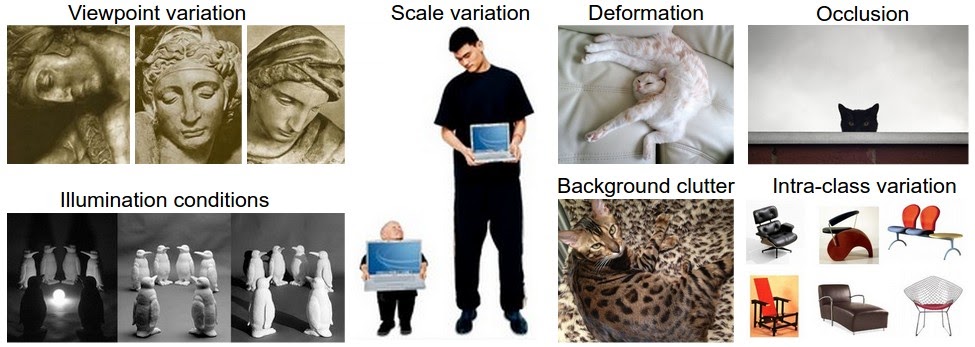
• Вариации точки зрения.  Один экземпляр объекта может быть ориентирован по-разному относительно камеры.
• Вариации масштаба. Визуальные классы часто демонстрируют вариации в своих размерах (размер в реальном мире, а не только в плане их протяженности на изображении).
• Деформация. Многие объекты интереса не являются твердыми телами и могут быть сильно деформированы.
• Препятствия. Объекты интереса могут быть закрыты. Иногда видна только небольшая часть объекта (всего несколько пикселей).
• Условия освещенности. Эффекты освещения очень сильны на пиксельном уровне.
• Шум заднего плана. Объекты интереса могут сливаться с окружающей средой, что затрудняет их идентификацию.
• Внутриклассовая вариация. Классы интересов часто могут быть относительно широкими, такими как стул. Существует много различных типов этих объектов, каждый из которых имеет свой собственный внешний вид.

Хорошая модель классификации изображений должна быть инвариантна к различным вариациям перечисленных выше проблем, сохраняя при этом чувствительность к межклассовым различиям.

Data-driven подход

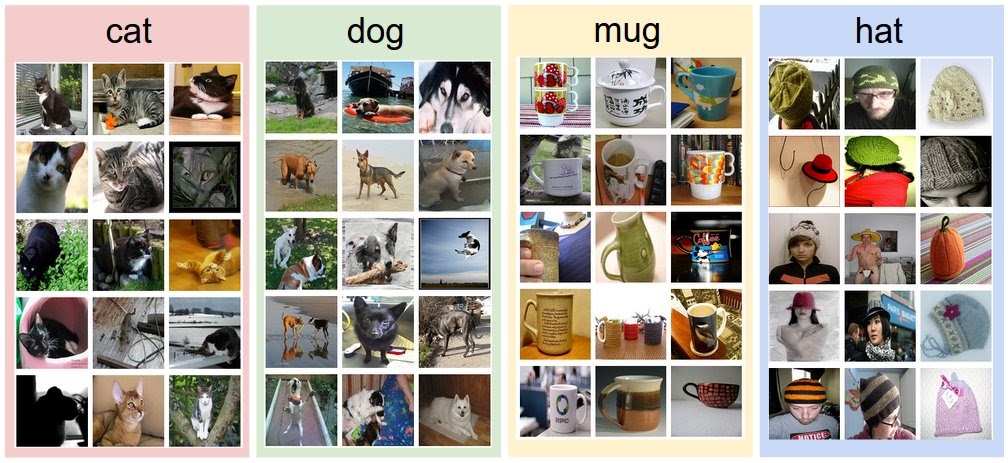
Как можно написать алгоритм, который сможет классифицировать изображения? В отличие от написания алгоритма, например, сортировки списка чисел, не очевидно, как можно написать алгоритм для идентификации кошек на изображениях. Поэтому вместо того, чтобы пытаться определить, как каждая из интересующих категорий выглядит непосредственно в коде, подход, который мы примем, не отличается от того, который используется с детьми: компьютеру предоставляется много примеров каждого класса, а затем разработанные алгоритмы обучения, “смотрят” на эти примеры и узнают о визуальном облике каждого класса. Этот подход называется data-driven подход, поскольку он основан на накоплении обучающего набора данных размеченных изображений. Ниже представлен пример того, как может выглядеть такой набор данных:

Этапы классификации изображений

Задача классификации изображений состоит в том, чтобы взять массив пикселей, представляющий одно изображение, и присвоить ему метку. Все этапы могут быть формализованы следующим образом:

• Ввод: входные данные состоят из набора N изображений, каждое из которых помечено одним из K различных классов.Эти данные называются обучающей выборкой.
• Обучение: задача состоит в том, чтобы использовать обучающую выборку, для выяснения, как выглядит каждый из классов. Этот шаг называется обучением классификатора или обучением модели.
• Оценка:  в конце концов, оценивается качество классификатора, путем попыток предсказания меток для нового набора изображений, которые не присутствовали в обучающей выборке. После чего сравниваются истинные метки этих изображений с предсказанными классификатором. Хорошо обученный классификатор должен обеспечить то, что многие предсказания совпадут с правдивыми ответами (которые называются истинными).

Классификатор Nearest Neighbor

В качестве первого подхода рассмотрим то, что называется Nearest Neighbor классификатором. Этот классификатор не имеет ничего общего со сверточными нейронными сетями и очень редко используется на практике, но он позволит получить представление об основном подходе к задаче классификации изображений.

Пример набора данных для классификации изображений: CIFAR-10

Одним из популярных наборов данных классификации изображений игрушек является набор данных CIFAR-10. Этот набор данных состоит из 60 000 крошечных изображений высотой и шириной 32 пикселя. Каждое изображение помечается одним из 10 классов (например, ”самолет, автомобиль, птица и т. д.»). Эти 60 000 изображений разбиты на обучающую выборку и тестовую из 50 000 и 10 000 изображений, соответственно. На рисунке ниже вы можете увидеть 10 случайных примеров изображений из каждого из 10 классов:

Предположим, что нам дан обучающий набор CIFAR-10 из 50 000 изображений  (5000 изображений для каждой метки), и мы хотим пометить оставшиеся 10 000. Классификатор возьмет тестовое изображение, сравнит его с каждым из обучающих изображений и предскажет метку на основе ближайшего обучающего изображения. На рисунке выше справа вы можете увидеть пример результата такой процедуры для 10 примеров тестовых изображений. Обратите внимание, что только в 3 из 10 примеров извлекается изображение того же класса, в то время как в остальных 7 примерах это не так. Например, в 8-м ряду ближайшим тренировочным изображением к голове лошади является красный автомобиль, предположительно из-за сильного черного фона. В результате этот образ лошади в данном случае будет неверно обозначен как автомобиль.

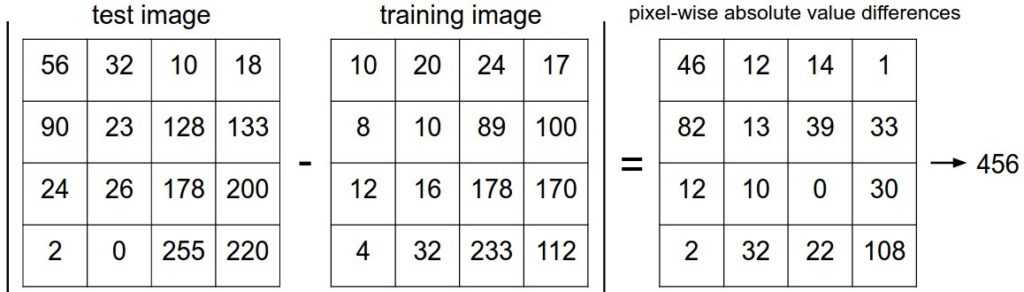
Вы, возможно, заметили, что детали того, как именно сравниваются два изображения, которые в данном случае являются просто двумя блоками 32x32x3, остались не рассмотренными. Один из самых простых путей — сравнить изображения пиксель за пикселем и сложить все различия. Другими словами, даны два изображения и представление их в виде векторов \( I_1\), \( I_2\), разумным выбором для их сравнения может быть расстояние L1:

\[ d_1 (I_1, I_2) = \sum_{p} \left| I^p_1 — I^p_2 \right| \]

Где сумма берется по всем пикселям. Визуализация процедуры:

Рассмотрим, как можно реализовать классификатор в коде. Во-первых, загрузим данные CIFAR-10 в память в виде 4 массивов: обучающие данные/метки и тестовые данные/метки. В приведенном ниже коде Xtr (размером 50 000x32x32x3) содержит все изображения в обучающем наборе, а соответствующий 1-мерный массив Ytr (длиной 50 000) содержит обучающие метки (от 0 до 9):

Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # волшебная функция, которую мы предоставляем
# выравнить все изображения, чтобы они были одномерными
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows станет  50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows станет 10000 x 3072

Теперь, когда у есть все изображения, представленные в виде строк, вот так можно обучить и оценить классификатор:

nn = NearestNeighbor() # создание класса Nearest Neighbor классификатор
nn.train(Xtr_rows, Ytr) # обучение классификатора на обучающем наборе изображений и меток
Yte_predict = nn.predict(Xte_rows) # предсказание меток на тестовом наборе
# и теперь вывод точности классификатора, которая яввляется средним числом
# верно предсказанных  примеров (т.е. метки совпадают)
print( 'accuracy: %f'%( np.mean(Yte_predict == Yte)))

Обратите внимание, что в качестве критерия оценки обычно используется точность, которая измеряет долю правильных прогнозов. Также стоит заметить, что все классификаторы, которые мы построим, удовлетворяют общему API: у них есть функция train(X,y), которая принимает данные и метки, чтобы учиться. Внутри класс должен построить некоторую модель меток и того, как они могут быть предсказаны из данных. А также есть функция predict(X), которая берет новые данные и предсказывает метки. Конечно, упущено самое главное — собственно классификатор. Ниже представлена реализация простого Nearest Neighbor классификатора с расстоянием L1, который удовлетворяет этому шаблону:

import numpy as np

class NearestNeighbor(object):
  def __init__(self):
    pass

  def train(self, X, y):
    """ X это N x D где каждая строка это пример. Y это 1-измерение размера N """
    # nearest neighbor классификатор просто запоминает весь обучающий набор
    self.Xtr = X
    self.ytr = y

  def predict(self, X):
    """ X это N x D где каждая строка это пример для которого необходимо определить метку """
    num_test = X.shape[0]
    # убедимся в том, что выходные типы совпадают с входными
    Ypred = np.zeros(num_test, dtype = self.ytr.dtype)

    # цикл по всем строкам теста
    for i in xrange(num_test):
      # найдите ближайшее обучающее изображение к i-му тестовому изображению
      # используя расстояние L1 (сумма разностей абсолютных значений)
      distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
      min_index = np.argmin(distances) # получить индекс с наименьшим расстоянием
      Ypred[i] = self.ytr[min_index] # предсказать метку ближайшего примера

    return Ypred

Если запустить этот код, вы увидите, что данный классификатор достигает только 38,6% точности на CIFAR-10. Это лучше, чем предсказание наугад (что дало бы точность 10%, так как есть 10 классов), но далеко от человеческой (которая оценивается примерно в 94%) или от современных сверточных нейронных сетей, которые достигают около 95%, соответствуя человеческой точности (см. таблицу лидеров конкурса Kaggle на CIFAR-10).

Выбор расстояния

Существует множество других способов вычисления расстояний между векторами. Другим распространенным выбором может быть использование расстояния L2, которое имеет геометрическую интерпретацию вычисления евклидова расстояния между двумя векторами. Расстояние принимает форму:

\[ d_2 (I_1, I_2) = \sqrt{\sum_{p} \left( I^p_1 — I^p_2 \right)^2} \]

Другими словами, будет вычисляться разница в пикселях, как и раньше, но на этот раз разница возводится в квадрат, складывается и, наконец, извлекается квадратный корень. Благодаря numpy, нужно будет заменить только одну строку кода. Строку, которая вычисляет расстояния:

distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))

Заметьте, что добавлен вызов np.sqrt, но в практическом приложении Nearest Neighbor можно было бы опустить операцию квадратного корня, потому что квадратный корень — монотонная функция. То есть он масштабирует абсолютные размеры расстояний, но сохраняет порядок, поэтому ближайшие соседи с ним или без него идентичны. Если бы вы запустили классификатор ближайших соседей на CIFAR-10 с этим расстоянием, вы получили бы точность 35,4% (немного ниже, чем результат расстояния L1).

L1 против L2. Интересно рассмотреть различия между этими двумя показателями. В частности, расстояние L2 гораздо более чувствительна, чем расстояние L1, при оценке разницы между двумя векторами. То есть при использовании L2 предпочтительнее множество средних расхождений одному большому. Расстояния L1 и L2 (или, что эквивалентно, нормы L1/L2 расстояний между парой изображений) являются наиболее часто используемыми частными случаями p-нормы.

k — Nearest Neighbor Классификатор

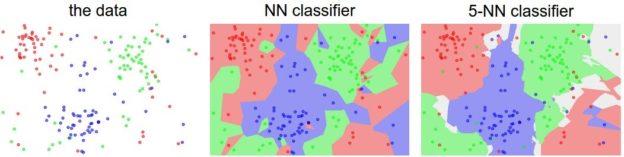
Возможно, вы заметили, что странно использовать класс только ближайшего изображения только тогда, когда мы хотим сделать предсказание. Действительно, почти всегда бывает так, что можно сделать более качественное предсказание, используя то, что называется классификатором k — Nearest Neighbor(k — ближайших соседей). Идея очень проста: вместо того, чтобы найти единственное ближайшее изображение в обучающем наборе, мы найдем k ближайших изображений и на основе их классов выберем метку тестового изображения. В частности, при k = 1 мы имеет Nearest Neighbor классификатор. Интуитивно понятно, что более высокие значения k имеют сглаживающий эффект, что делает классификатор более устойчивым к выбросам:

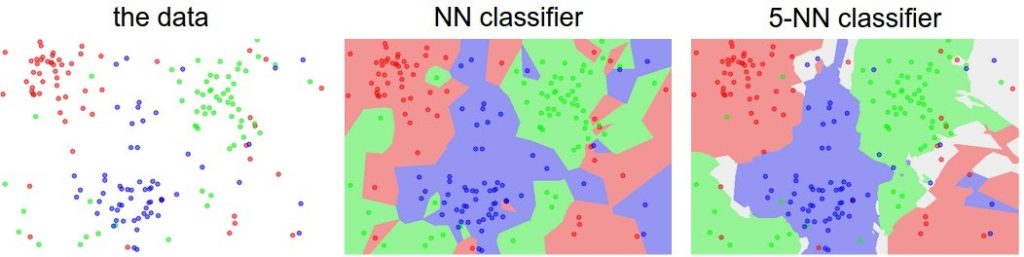
На практике почти всегда используется k — Nearest Neighbor. Но какое значение k следует использовать? Мы вернемся к этой проблеме в дальнейшем.

Настройка гиперпараметров

Классификатор k-ближайших соседей требует установки значения k. Но какое число будет наиболее оптимальным? Кроме того, есть много различных функций вычисления расстояния, которые можно использовать: L1 норма, L2 норма, а также много других вариантов, которые не рассматривались (например: скалярное произведение). Эти варианты называются гиперпараметрами, и они очень часто возникают при разработке алгоритмов машинного обучения. Часто не очевидно, какие значения или настройки следует выбрать.

Возможно, у вас возникнет соблазн опробовать множество различных значений и посмотреть, что работает лучше всего. Это прекрасная идея, и именно так мы и поступим, но делать это нужно очень осторожно. В частности, мы не можем использовать тестовый набор для настройки гиперпараметров. Всякий раз, когда вы разрабатываете алгоритмы машинного обучения, вы должны думать о тестовом наборе как об очень ценном ресурсе, который в идеале должен быть затронут единственный раз, в самом конце обучения. В противном случае опасность заключается в том, что вы можете настроить гиперпараметры так, чтобы они хорошо работали на тестовом наборе, но при развертывании модели на реальных данных, вы увидите значительно сниженную производительность. На практике мы бы сказали, что модель переобучилась на тестовый набор. Иными словами, если настраивать гиперпараметры на тестовом наборе, вы будете использовать его в качестве обучающего набора, и поэтому производительность, которой вы достигнете, будет слишком оптимистичной по отношению к тому, что вы могли бы реально наблюдать при развертывании модели. Но если использовать тестовый набор только один раз в конце обучения, он остается доверенным множеством для измерения обобщения Классификатора

Используйте тестовый набор только один раз, в конце обучения.

К счастью, существует другой способ настройки гиперпараметров, который не использует тестовый набор. Идея состоит в том, чтобы разделить наш обучающий набор на два: тренировочное множество и то, что называется проверочным множеством (validation set). Используя CIFAR10 в качестве примера, мы могли бы, например, использовать 49 000 обучающих изображений для обучения, а 1000 оставить для проверки. Это проверочное множество по существу используется в качестве поддельного набора тестов для настройки гиперпараметров.

Вот как это будет выглядеть в случае CIFAR-10:

# предположим у нас есть Xtr_rows, Ytr, Xte_rows, Yte как ранее
# напомним Xtr_rows - это матрица размером 50,000 x 3072
Xval_rows = Xtr_rows[:1000, :] # возьмем 1000 для проверки
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # оставшиееся 49,000 для обучения
Ytr = Ytr[1000:]

# найдем лучшие гиперпараметры для проверочного множества
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:
  
  # используем конкретное значение k и оценку по проверочному набору
  nn = NearestNeighbor()
  nn.train(Xtr_rows, Ytr)
  # здесь мы принимаем модифицированный класс NearestNeighbor, который может использовать k в качестве параметра
  Yval_predict = nn.predict(Xval_rows, k = k)
  acc = np.mean(Yval_predict == Yval)
  print 'accuracy: %f' % (acc,)

  # проследим работу на проверочном множестве
  validation_accuracies.append((k, acc))

К концу этой процедуры можно построить график, который покажет, какие значения k работают лучше всего. Затем мы оставляем это значение и один раз проводим оценку на актуальном наборе тестов.

Разделите обучающий набор на тренировочный и проверочный. Используйте проверочный набор для настройки всех гиперпараметров. В конце запустите один раз тестовый набор и сделайте вывод о качестве модели.

Cross-validation

В случаях, когда размер обучающих данных (а следовательно, и проверочных данных) может быть небольшим, иногда используют более сложную технику настройки гиперпараметров, называемую перекрестной проверкой (Cross-validation). Используем наш предыдущий пример, идея заключается в том, что вместо произвольного выбора первых 1000 точек данных для проверочного множества, вы можете получить лучшую и менее шумную оценку того, насколько хорошо работает определенное значение k, повторяя различные проверочные множества и усредняя производительность по ним. Например, при 5-кратной перекрестной проверке мы разделили бы обучающие данные на 5 равных частей, использовали бы 4 из них для обучения и 1 для проверки. Затем будем повторять эту процедуру, изменяя часть, которая является проверочной, после оценим производительность и, наконец, усредним производительность по различным частям.

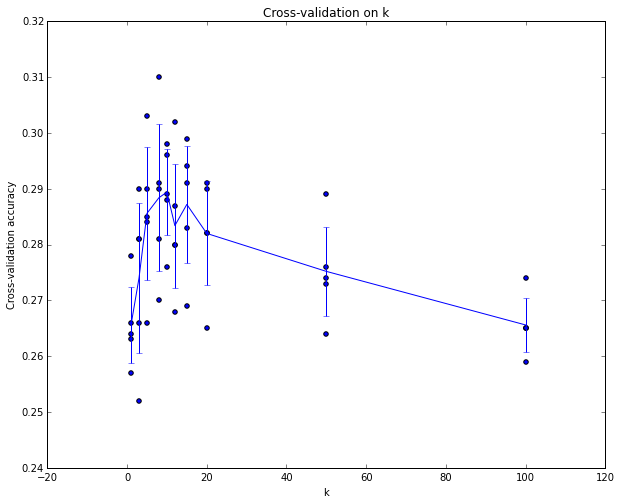
На практике стараются избегать перекрестной проверки в пользу использования единственного разделения, так как перекрестная валидация может быть вычислительно дорогостоящей. Разбиения, которые обычно используют, составляют от 50% до 90% тренировочных данных для обучения и остальное для проверки. Однако это зависит от нескольких факторов: например, если число гиперпараметров велико, вы можете предпочесть использовать более крупные проверочные разбиения. Если число примеров в наборе проверки невелико (возможно, всего несколько сотен или около того), то безопаснее использовать перекрестную проверку. Типичное количество разделяемых частей, которое используется на практике, будет 3-кратная, 5-кратная или 10-кратная перекрестная проверка.

Плюсы и минусы классификатора ближайших соседей

Стоит рассмотреть некоторые преимущества и недостатки классификатора ближайших соседей. Ясно, что одним из преимуществ является то, что его очень просто реализовать и понять. Кроме того, классификатор не требует времени для обучения, так как все, что требуется, — это хранить и, возможно, индексировать обучающие данные. Однако мы расплачиваемся за эту  экономию вычислительных затрат во время использования, поскольку классификация тестового примера требует сравнения с каждым отдельным обучающим примером. Это обратная сторона, так как на практике мы часто заботимся об эффективности времени использования гораздо больше, чем об эффективности во время обучения. На самом деле, глубокие нейронные сети, которые мы будем рассматривать позже в этом курсе, переносят этот компромисс в другую крайность: они очень дороги для обучения, но как только обучение закончено, очень дешево классифицировать новый тестовый пример. Этот режим работы гораздо более желателен на практике.

Кроме того, вычислительная сложность классификатора ближайшего соседа является активной областью исследований, и существует несколько приближенных алгоритмов и библиотек (Approximate Nearest Neighbor/ANN), которые могут ускорить поиск ближайшего соседа в наборе данных (например, FLANN). Эти алгоритмы позволяют компенсировать корректность поиска ближайшего соседа его размерно/временной сложностью во время поиска и обычно полагаются на стадию предварительной обработки/индексирования, которая включает в себя построение kdtree или запуск алгоритма k-means.

Классификатор ближайших соседей иногда может быть хорошим выбором в некоторых случаях (особенно если данные являются низкоразмерными), но он редко подходит для использования в практических ситуациях классификации изображений. Одна из проблем заключается в том, что изображения являются многомерными объектами (т. е. они часто содержат много пикселей), а расстояния в многомерных пространствах могут быть очень противоречивыми. Изображение ниже иллюстрирует тот момент, что пиксельные сходства L2, которые мы разработали выше, очень отличаются от перцептивных сходств:

Вот еще одна визуализация, которая убедит вас в том, что использование различий пикселей для сравнения изображений является недостаточным. Мы можем использовать технику визуализации, называемую t-SNE, чтобы взять изображения CIFAR-10 и встроить их в два измерения так, чтобы их (локальные) попарные расстояния лучше всего сохранялись. В этой визуализации изображения, которые показаны рядом, считаются очень близкими в соответствии с пиксельным расстоянием L2, которое мы разработали выше:

В частности, обратите внимание, что изображения, которые находятся рядом друг с другом, гораздо больше зависят от общего цветового распределения изображений или типа фона, чем от их семантической идентичности. Например, собаку можно увидеть совсем рядом с лягушкой, так как обе они находятся на белом фоне. В идеале мы хотели бы, чтобы изображения всех 10 классов образовывали свои собственные кластеры, так чтобы изображения одного и того же класса находились рядом друг с другом независимо от несущественных характеристик и вариаций (таких как фон). Однако, чтобы получить это свойство, нам придется выйти за рамки простых характеристик пикселей.

Заключение

• Мы ввели задачу классификации изображений, в которой нам дается набор изображений, которые все помечены одной категорией. Затем нас просят предсказать эти категории для нового набора тестовых изображений и измерить точность предсказаний.
• Мы ввели простой классификатор, называемый классификатором ближайших соседей (Nearest Neighbor classifier). Мы видели, что существует множество гиперпараметров (таких как значение k или тип расстояния, используемого для сравнения примеров), которые связаны с этим классификатором, и не нашли очевидного способа их выбора.
• Мы увидели, что правильный способ установить эти гиперпараметры — разделить ваш обучающие набор на два: тренировочный набор и поддельный набор тестов, который называется проверочным набором. Мы пробуем различные значения гиперпараметров и сохраняем значения, которые приводят к лучшей производительности в наборе проверки.
• Если существует проблема отсутствия обучающих данных, мы обсудили процедуру, называемую перекрестной проверкой, которая может помочь уменьшить шум при оценке того, какие гиперпараметры работают лучше всего.
• Как только лучшие гиперпараметры найдены, мы фиксируем их и выполняем единственную оценку на актуальном наборе тестов.
• Мы видели, что ближайший сосед может дать нам около 40% точности на CIFAR-10. Он прост в реализации, но требует, чтобы мы хранили весь учебный набор, и это затратно, для оценки тестового изображения.
• Наконец, мы увидели, что использование расстояний L1 или L2 для простых характеристик пикселей не является адекватным, поскольку расстояния коррелируют более сильно с фоном и цветовыми распределениями изображений, чем с их семантическим содержанием.

В следующих частях мы приступим к решению этих проблем и в конечном итоге придем к решениям, которые дают точность 90%, позволяют полностью отказаться от обучающего набора после завершения обучения, и способны оценить тестовое изображение менее чем за миллисекунду.

Вывод: применение kNN на практике

Если вы хотите применить kNN на практике (надеюсь, не на изображениях или, возможно, только в качестве ознакомления), действуйте следующим образом:

1. Предварительно обработайте данные: нормализируйте  особенности данных (например, один пиксель в изображениях) чтобы получить нулевое среднее значение и единичную дисперсию. Мы рассмотрим это более подробно в последующих разделах и решили не рассматривать нормализацию данных в этом разделе, поскольку пиксели на изображениях обычно однородны и не демонстрируют сильно отличающихся распределений, что облегчает необходимость нормализации данных.
2. Если ваши данные очень многомерны, рассмотрите возможность использования метода уменьшения размерности, такого как PCA (wiki ref, CS229ref, blog ref) или даже случайных проекций.
3. Разделите обучающий набор в произвольном порядке на тренировочный/проверочный. Как правило, 70-90% ваших данных, идет в тренировочный набор. Эта настройка зависит от того, сколько гиперпараметров у вас есть и какое влияние вы ожидаете от них. Если существует много гиперпараметров для оценки, вы должны ошибиться в сторону эффективной оценки наибольшего набора проверки. Если вас беспокоит размер ваших проверочных данных, лучше всего разделить обучающие данные на части и выполнить перекрестную проверку. Если вы можете позволить себе использовать вычислительные мощности, то всегда безопаснее использовать перекрестную проверку (чем больше частей, тем лучше, но дороже).
4. Обучите и оцените классификатор kNN по проверочным данным (для всех частей, если делать перекрестную-валидацию) для многих вариантов k (например, чем больше, тем лучше) и через различные типы расстояний (L1 и L2-хорошие кандидаты)
5. Если ваш классификатор kNN работает слишком долго, рассмотрите возможность использования приближенных  алгоритмов ближайшего соседа (например, библиотеку FLANN) для ускорения поиска (ценой некоторой точности).
6. Обратите внимание на гиперпараметры, которые дают наилучшие результаты. Возникает вопрос, следует ли использовать полный тренировочный набор с лучшими гиперпараметрами, поскольку оптимальные гиперпараметры могут измениться, если вы вложите проверочные данные в свой обучающий набор (поскольку размер данных будет больше). На практике правильнее не использовать валидационные данные в конечном классификаторе и считать их сожженными при оценке гиперпараметров. Оцените лучшую модель на тестовом наборе. Сообщите о точности оценки тестового набора и объявите результат как производительность классификатора kNN на ваших данных.