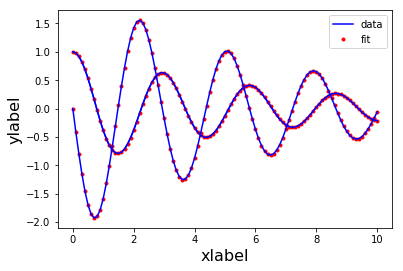
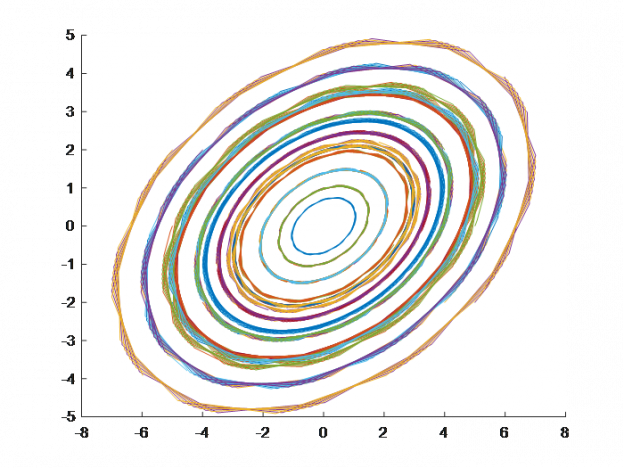
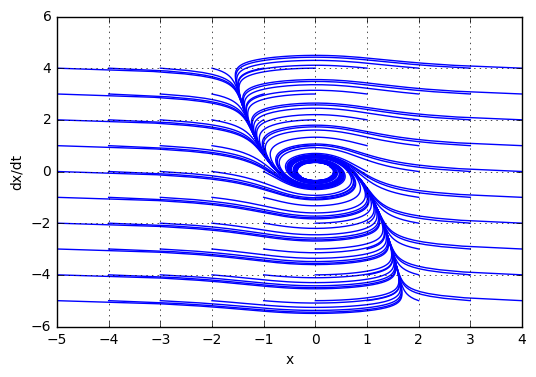
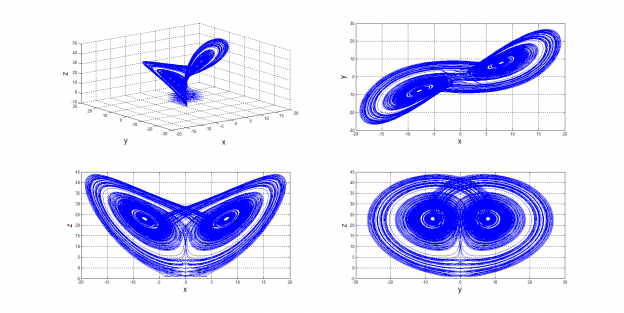
Одной из распространенных задач, возникающих при исследовании различных объектов — построение математической модели. Нередко математическая модель представляется в виде системы дифференциальных уравнений, однако непосредственное измерение всех, входящих в них параметров, как правило, невозможно по различным причинам. В таком случае, одним из подходов является проведение идентификационных экспериментов и оценка параметров ДУ путем решения оптимизационной задачи.
В статье рассмотрен простой способ оценки параметров системы ДУ в форме Коши на языке Python.